-
The folder /TopologyOptimizatoinToolbox contains all the Matlab functions
-
The folder /Examples contains files required for some of the examples
-
The matlab files strarting with MI are examples in which the mesh files are imported from the /Examples folder.
-
The matlab files starting with MG are examples in which the mesh is generated by the topology optimization toolbox. These take longer to run as the mesh has to be generated. It is not recomended to generate meshes with more that 200 000 nodes as the optimization might take too long.
-
The most complete example is MG_simpleHinge.
-
The fastest example(with a reasonable number of elments) is MI_thinBeam.
-
Each time the optimization is run, two folders will be created under
/RESULTS/<folderName>and/ITERATIONS/<folderName>with the optimization results and with figures of each iteration.
The first step in the optimization is to obtain a mesh of the design domain. As
we are using TET4 elements, this mesh will be stored as two arrays: nodeCoord
(Stores the coordinates of each node in a numNodes by 3 array) and elemConn
(Stores the nodes that compose each element in a numElem by 4 array). These two
arrays will be two of the properties of the rMesh object that is used in this project.
In order to generate such object, there are two methods depending on the source of
the mesh. These are specified through the mesh-settings structure array that is the
only argument of the rMesh constructor.
The mesh can be generated with the provided functions. In order to do this, the
mesh-Settings structure array must either not have a feld name import or have it
set as false. The dimensions of the mesh and the element size are specifed with the
values of Lx, Ly, Lz, and d. These are the most important parameters that defne
the mesh that will be generated; the rest of the values of the mesh-settings structure
array can be loaded from the defaultMeshSettings() function(Before setting
any values in order to not overwrite them). The following example generates a mesh
of dimensions 2 by 1 by 1 with an element size of 0.04.
1 mS = defaultMeshSettings(); % Mesh Settings struct with default values
2 mS.Lx = 2; mS.Ly = 1; mS.Lz = 1; % Dimensions
3 mS.d = 0.04; % Element Size
4 m = rMesh(mS); % Generates rMesh Object
The mesh can also be imported by setting a field of the mesh-settings structure
array named import to true and setting the fileName field to the name of the
Optistruct .fem file that contains the mesh. This does not, however, import loads or
boundary conditions that may have been stored in this file. The following example
imports the mesh stored in Examples/example2.fem.
1 mS.import = true;
2 mS.fileName = 'Examples/example2.fem';
3 m = rMesh(mS);
Once the rMesh object is generated, its functions can be used to, for example, plot the mesh. The command m.plot will plot all elements of the mesh. Additional arguments and functionality can be explored by typing help m.plot.
The generated rMesh object has several other methods and properties that are very
useful to modify the design domain for the optimization. First of all, m.X, m.Y,
m.Z, m.numElem and m.numNodes receive no arguments and return the nodal X,
Y and Z coordinates, the number of elements and the number of nodes respectively.
Furthermore, the rMesh object has two more useful properties m.nonDesign
and m.zeroElements which are a list of elements that cannot be modifed in
the optimization. The frst of these is a list of elements which must have a den-
sity equal to one; this is useful with elements near boundary conditions as elements
that have a load applied on one of their nodes will always have a density equal to 1.
The second of these properties is a list of elements which must have a density
equal to either zero or the minimum value specifed later on in the optimization
settings structure array ; this is useful in order to remove elements in a certain area
of the design domain. Each of these properties is modifed by using the functions
m.nonDesignElements(condition) and m.removeElements(condition).
The argument condition is a logical array of size number of nodes by one. For each
true or 1 value in this array, all the elements that contain the corresponding node
will be considered as satisfying the condition and therefore added to either the ze-
roElements array or the nonDesign array. The following example removes a cylinder
from the design domain, sets some elements as non-Design domain(density always
equal to one), plots the mesh and plots the non-Design elements diferently:
1 m.removeElements((m.X - 1.5).ˆ2 + (m.Z - 0.5).ˆ2 < 0.2.ˆ2)
2 m.nonDesignElements( (m.X < 0.5) & (m.Z == 0) )
3 figure(1)
4 m.plot; hold on
5 m.plotNonDesign
6 title('Design Domain')
In order to specify the loads and boundary conditions on the nodes of the generated mesh, the following command must be run in order to generate a femObject instance. The only argument required for the constructor method is the previously generated rMesh object.
1 f = femObject(m);
The boundary conditions are added by using the funciton f.addBC(direction, condition). The first argument specifes the direction in which the movement is
restricted and can be one of the following 'X', 'Y', 'Z' and 'XYZ'(All directions).
The second argument is a logical array of size number of nodes by one; nodes which
have a true or 1 value will be restricted in the specifed direction or directions.
The loads are added with the f.addLoad(direction, value) function. The
frst argument specifes the load direction and can be one of the following 'X', 'Y',
and 'Z' (Not 'XYZ'). The second argument specifes the load, positive or negative
depending on the direction on each node and is therefore a number of nodes by 1
array. Elements which have nodes with non-zero loads will automatically be added
to the non-design space elements(even though they will not be plotted diferently
with m.plotNonDesign).
The f.plot(type, direction, color) function will display the loads and
boundary conditions by specifying the type argument as either 'bound' or 'load',
direction argument to 'X', 'Y', 'Z' or '[]' (all directions) and the color argument as
the color for each type of plot. The following code adds some loads and boundary
conditions and plots these in different directions:
1 f.addBC('XYZ', (m.X < 0.5) & (m.Z == 0) & (abs(m.Y - 0.5) > 0.2))
2
3 q1 = abs((m.X - 1.5).ˆ2 + (m.Z - 0.5).ˆ2 -0.2ˆ2) < 0.08.ˆ2; % Condition 1
4 q2 = abs(m.Y - 0.5) < 0.15; % Condition 2
5 p = -1000./sum(q1.* q2); % Magnitude
6 f.addLoad('Z', p.* q1.* q2)
7 hold on
8 f.plot('load', 'Z', 'r')
9 f.plot('bound', [], 'b')
10 title('Design Domain, Loads and Boundary Conditions')
The strain stress law must be specified using f.addMaterial(C), the follow- ing example uses the strainStressLaw() function to generate the compliance matrix for an isotropic material and adds it to the femObject instance.
1 E = 200e9;
2 nu = 0.3;
3 C = strainStressLaw(E, nu);
4 f.addMaterial(C)
First of all, the optimization settings structure array has to be generated; this can be
done manually or by using the defaultOptimSettings() function. The most
important fields are Vstar, numIter, method and, if the BESO method is being
used extraIter.(This corresponds to the number of iterations without a change in
volume after the objective volume has been reached. Using the femObject instance
and the optimization settings structure array, the optimizationObject constructor
can be called. Once the optimizationObject instance is created, the optimization can
be run with optimizationObject.startOptimization(f1, f2, name).
It can also be run without arguments; f1 and f2 are the figure numbers for the plot
that will be generated on each iteration and the final results plot respectively. The
third argument is a string that will define the name of the folder in which the results
will be stored; if it is not specified, the current date and time will be the name of
the folder.
1 os = defaultOptimSettings();
2 os.Vstar = 0.25; % Objective Volume
3 os.numIter = 25; % Number of Iterations
4 os.method = 'SIMP'; % Optimization Method
5
6 optimObj = optimizationObject(f, os);
7
8 optimObj.startOptimization(2,3,'simpleHinge')
Once the optimization algorithm has finished, it will display the outside surface plot, save the workspace and figures in RESULTS/'name' and save a '.stl' file of the outside surface in the same folder.
The optimizationObject() instance has a series o functions that help with the post- processing of the results both for analysis and for exporting the results.
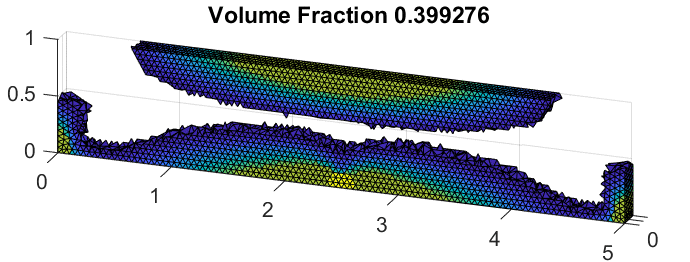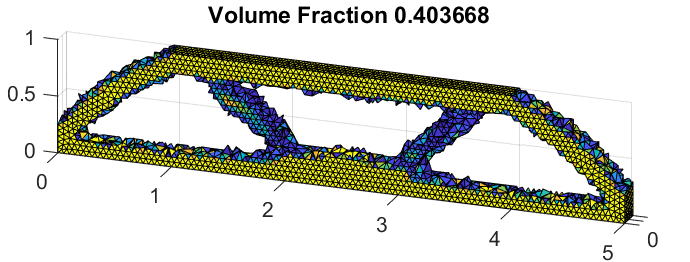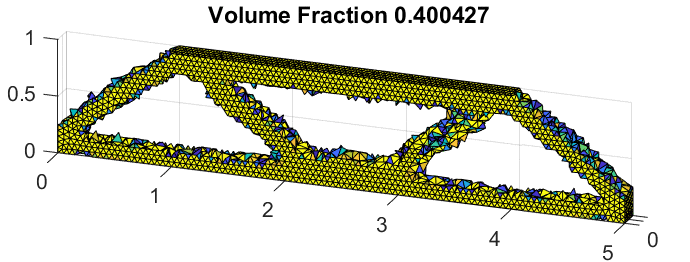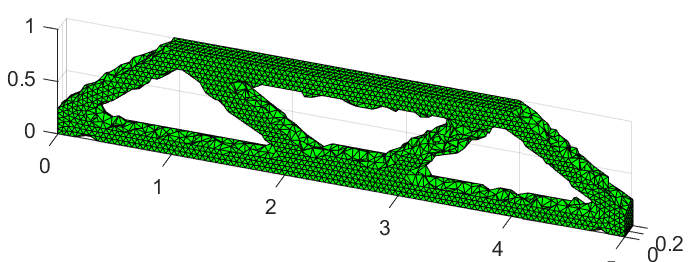
The following function plots the outside surface of the solution and (optionally) returns five values: the volume contained within the outside surface, a triangular mesh element connectivity array and each of the three coordinates of the nodes that form the outside surface. All arguments are optional; the first input argument, cutoff, is the partial density value above which elements are considered part of the solution, if unspecified, it uses the cutoff value from the optimization settings structure array. The second argument, shrinkFactor de ne how tightly the outside surface wraps around the solution; if unspeci ed, the default value is 0.85. This argument is used for Matlab's boundary() function and is referenced in the o�cial Matlab documentation under the boundary() function. The third and last argument, 'plotType' is used to color the surface depending on the value of one of the coordinates; its possible values are therefore 'X', 'Y', 'Z', and 'N' (none, same as avoiding this argument, plots the whole surface in green). Coloring the outside surface with a color that depends on a coordinate is done simply to be able to better see the geometry.
1 figure(4)
2 [V, sConn, X0, Y0, Z0] = optimObj.boundary1([], [], 'Y');
3 colormap jet
The optimObj.calculateStresses function calculates the stress tensor in Voigt nota-
tion and the Von-Misses equivalent stress for each element. These are stored in the
VM and stress properties of the optimization object.
The function optimObject.plot(plotType, direction) generates a plot
of the current solution. If no arguments are given, the plot obtained is identical
to that of the last iteration. If the first argument is 'D', the elements will be
colored according to the average displacement of their nodes in the direction specified
by the second argument; this argument can be either 1:(X-Dsiplacements), 2:(Y-
Displacements) or 3:(Z-Displacements). If the first argument is 'S', the elements will
be colored acording to the element of the stress tensor in Voigt notation specified
by the second argument (1:Sigma-x, 2:Sigma-y, 3:Sigma-z, 4:Tau-yz, 5:Tau-xz, 6:Tau-xy).
Finally, if the firstargument is 'VM', elements will be colored according to their
Von-Misses stress.
1 figure(5)
2 optimObj.plot('VM')
3 set(gca,'ColorScale','log')
4
5 figure(6)
6 optimObj.plot('S', 1)
7
8 figure(7)
9 optimObj.plot('D', 3)