Aunque regresión lineal nos ayuda resolver muchos problemas, no es la mejor opción cuando nos enfrentamos a problemas de clasificación. Clasificar data points es uno de los trabajos más comunes de los data scientists.
En este apunte encontrarás la explicación teorica y matemática de la clasificación lineal. En los apuntes, pasamos al código para ilustrar los temas cubiertos acá. Para este propósito usamos los data sets de Iris y Pingüinos que pertenecen a la librería Seaborn.
Si tienes alguna pregunta, no dudes en contactarme en Twitter: @XaviGrowth
Nota 1: La notación para vectores es en negritas. Es decir, podrás identificar a los vectores cuando aparezcan de la siguiente manera: y.
Uno de los problemas con los datos es que no siempre hay una continuidad entre ellos. En estos casos nos referimos a un problema que no se puede explicar cuantitativamente sino cualitativamente. Es decir, los problemas de clasificación. Lidiar con ellos usando regresión linear es complicado, por lo que es necesario ocupar otras técnicas.
El propósito de Machine Learning es predecir valores desconocidos a partir de datos históricos. Imaginemos que tenemos un problema en el que hay datos de conejos, perros y pollos, con los cuales queremos entrenar a nuestro modelo para predecir animales por nosotros. Una regresión linear no sirve en estas circunstancias porque los valores son categóricos (cualitativos) en vez de numéricos.
Para el problema anterior, podríamos proponer dos soluciones:
- Poner etiquetas x1, x2 y x3 para identificar a cada uno de los animales.
- Podríamos crear una matriz con valores booleanos para identificar a los animales. Ergo (1,0,0), (0,1,0) y (0,0,1).
En este caso, el enfoque clásico de machine learning es utilizar valores booleanos porque no hay ninguna relación ordinal entre los animales. A esto también se le conoce como hot encoding. Esto hace más sencillo manipular e interpretar datos. Con esto podemos armar vectores que conformarán nuestra matriz. Si tuvieramos un conjunto de animales que fuera perro, pollo, conejo, pollo, nuestra matriz se vería de la siguiente forma:
[0 1 0]
[0 0 1]
[1 0 0]
[0 0 1]
Ahora tenemos una buena forma de representar clasificaciones, por lo que podemos hacer predicciones con variables predictoras.
El objetivo de un algoritmo de clasificación es encontrar la clase o etiqueta a la que pertence un data point. Podemos hacer esto estimando la pobabilidad de que dicho data point pertenezca a dicha clase y tomando la calse con el mayor valor. Para esto, necesitamos una función que resulte en un valor que cumpla con los criterios de clase y otra que resulte en un valor cercano a cero representando que cae fuera de estos criterios. Es decir, decide si un data point se ajusta a cierta clase. Esta función, curiosamente, puede ser construida con una regresión linear.
Empecemos creando una variable ficticia y para esta clase con cada punto en nuestro data set. La variable y representa si un punto representa a la clase. Se le asigna 1 si pertenece a la clase y 0 si no pertenece. Dicha función y sería equivalente a un variable a predecir en una línea de mejor ajuste. Esto se vería así:
Nos sirve utilizar la misma fórmula para regresión linear:
Sin olvidar el orden de los animales (conejos, perros, pollos), supongamos que queremos saber si un data point nuevo es un perro o no. Suponiendo que tenemos dos datos sobre los animales (tamaño en cms y peso en g), la matriz A con datos de entrenamiento con tres animales diferentes se vería así:
[50 2500]
[120 15000]
[35 8000]
El vector b para identificar a un perro se vería así:
[0]
[0]
[1]
Finalmente tendríamos que comparar el nivel en que cada data point se ajusta a varias clases. En este caso, integraríamos a x1 que representa el tamaño y x2 que representa el peso. A partir de esto, podríamos investigar sobre los datos de todos los conejos en la región y diseñar una función que los decribe de la siguiente manera:
f Perro(x) = 0.02x2 + 3x3 - 25
Si tuvieramos un nuevo animal que midiera 130 cms y pesara 17000 gramos, notaríamos fácilmente que lo podríamos clasificar como un perro dado que:
f Perro(Animal nuevo) = 0.02 · 17000 + 3 · 390 - 25 = 1485
lo cual es un valor por encima del valor que podría representar los datos de un conejo (por ejemplo, 45 cms y 2300 gramos) o un pollo (por ejemplo, 55 cms y 12000).
Aunque las funciones son útiles para clasificar, hay que tomar en cuenta que no son la mejor manera de medir probabilidades. Al ser una función linear, es capaz de resultar en valores mayores a uno y menores a cero. Esto no nos sirve si estamos midiendo probabilidades. Al presentar el problema de esta forma, podemos producir valores negativos o que son demasiado grandes.
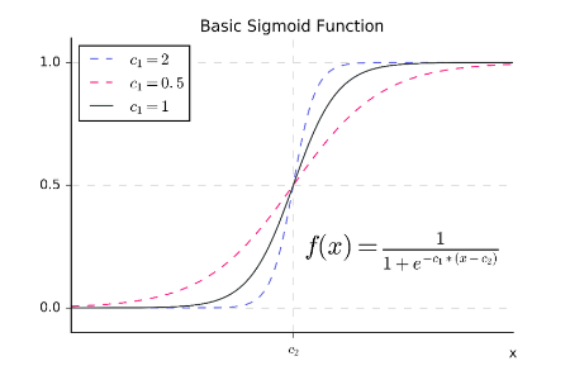
Transformar una función de clasificación lineal en una función de clasificación sigmoidal es muy útil cuando estamos trabajando con probabilidades.
Sin embargo, existe una forma de calcular una función sigmoidal de manera más directa. A esta se le conoce como la clasificación logística. Supopngamos que tenemos n cantidad de variables x1, x2,... xn usando una clasificación logística que calcula pesos m1, m2, ... mn y un sesgo en donde el sigmoide σ (m1x1 + m2x2 + ... mn xn + b) descibe bastante bien a nuestros datos.
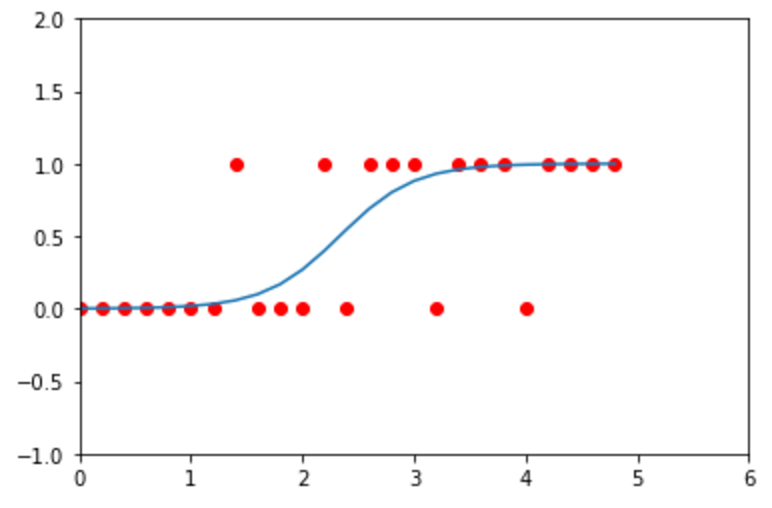
Un ejemplo sería el siguiente:
Acá hay una variable predictora y cada punto tiene un valor 1 cuando es cierto o 0 cuando es nulo. La sigmoide está diseñada para maximizar la probabilidad de clasificar correctamente entre dos clases. Esto es diferente a una clasificación con una matriz de indicadores, ya que hay una sola función para dos clases y no una función por cada clase.
Supongamos que queremos saber la probabilidad de que un alumno con promedio GPA de 3.2 (x1) y con 15 años de edad (x2) pase un examen, dado que los pesos de cada valor es de m1 = 5, m2 = 1 y el sesgo b = -29.
Utilizando la función de la sigmoide podemos ver que:
*f*(3.2, 15) = 5 ⋅ 3.2 + 1 ⋅ 15 - 29 = 2
σ(f(3.2,15)) = σ(2)
= e² / 1 + e²
= 0.88
Con la regresión logística creamos una función sigmoidal que describe nuestros datos. A esto tendríamos que agregar la propiedad de maximización.
Supongamos que tenemos dos clases: una positiva y una negativa. Para generar una función de mejor ajuste tenemos que analizar un conjunto de data points, los cuales sabemos que pertenecen a una de las dos clases. La función final (p x) nos dará la posibilidad de un x positivo.
Hay que tomar en cuenta que no todas las funciones de probabilidad son iguales. Hay que diferenciar entre calcular las probabilidades de nuestro data set dadas las clasificaciones y una función de probabilidad p(x) sea correcta. Esto significa usar p(x) para calcular la probabilidad de que cada data point esté en una clase y luego tomar los productos de los resultados.
Si asignamos a cada punto xi una variable yi que está puesta a 1 si x es positiva y 0 si es negativa, expresado matemáticamente, se vería así:
La probabilidad de que todos los puntos conocidos tengan una clase es lo que llamamos maximización en algoritmos de clasificación logística. El proceso es conocido como el método de máxima verosimilitud porque encontramos la similitud más posible en una función sigmoide.
Dado que la máxima verosimilitud es resultado de probabilidades, el techo siempre será 1 que significará una similitud exacta. Todas las probabilidades serán resultado de una función logística. Sin embargo, las probabilidades nunca serán 1 o 0.
Por ejemplo, si tenemos eventos independientes respecto a las probabilidades de sacar una bola roja entre bolas azules. Podríamos calcular las probabilidades tomando dos puntos en (3,2) y (-5,3). La probabilidad de sacar la bola roja es simplemente: 1 - p(x,y), lo que es igual a:
P = p(3, 2)(1 - p(-5,3))
= e⁶/1 + e⁶ ⋅ (1 - e⁻1/ 1 + e⁻1)
= 0.73
Hasta este momento hemos estimados las probabilidades de una regresión logística, más no como hacer una clasificación. Las clasificaciones son usualmente hechas poniendo un límite de probabilidades para dividir dos clases.
Por ejemplo, si clasificamos entre rojo y azul y los límites de probabilidad son p = 0.8. Los únicos puntos sobre el 80% serán clasificados como rojo. Por lo general los limites de probabilidad están basados en las necesidades de la situación. En situaciones reales, el límite puede ser bajo si el resultado no tiene grandes implicaciones. Pero si fuera el caso, habría que levantarlo por precaución (imagina si tuvieramos que determinar si una persona tiene una enfermedad seria o no).
Alternativamete, podríamos tomar una función logística y tranformarla en logarítmica. Tomando el logaritmo de una regresión logística nos da una función lineal que matemáticamente se ve así:
Esta función lineal se le conoce como logit. Aunque no es buena calculando probabilidades, es útil para comparasiones y optimizaciones. Esta es una alternativa cuando tenemos resultados extraños con una función logística.
Con regregresión lineal podemos predecir correctamente la clase a la que perenecen unos data points. Sin embargo, este enfoque puede ser inestable ya que genera una linea directamente de los datos.
Una alternativa es crear funciones de probabilidad basadas directamente en estadística. Aunque tenemos que hacer muchas suposiciones, el resultado final es una alternativa poderosa la clasificación logística.
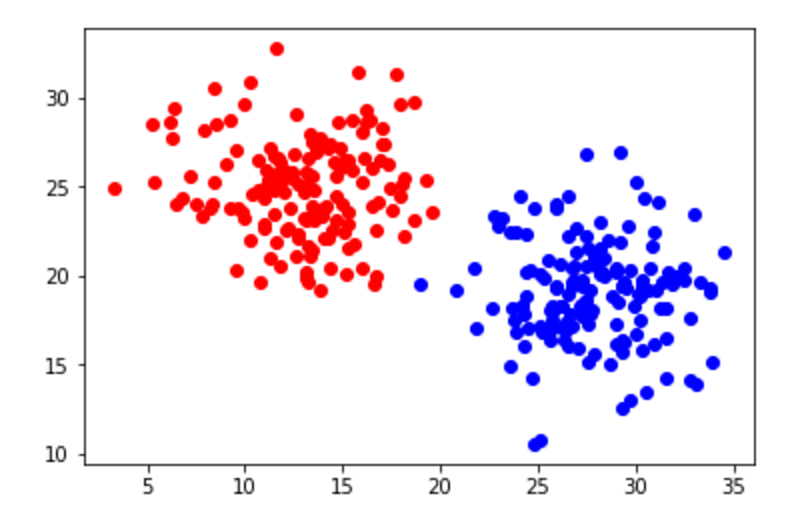
Primero, asumimos que nuetros data points pueden ser encontrados en una distribución gaussiana y que los puntos de diferentes clases tienen desviaciones estándard. Este conjunto de suposiciones nos dan una técninca de clasificación conocida como el análisis discriminante.
Acá tenemos un ejemplo de un data set con dos clases y dos variables predictoras que responderían bien a un análisis discriminante. Hay que notar que los puntos se separan de la clase. Esta es una indicación de que estamos tratando con una distribución gaussiana.
Acá es donde podemos usar el teorema de Bayes, que indica que dos eventos A y B son posibles.
Digamos que tenemos un punto x y queremos encontrar la probabilidad de que sea de la clase A. En este caso solo sabemos que:
- Sabemos que un punto aleatorio en la clase A tiene un 30% de posibilidades de ser igual a x.
- Sin ningún conocimiento previo, hay 50% de posibilidades de que un punto aleatorio sea x.
- Hay 10% de posibilidad que el punto aleatorio este en clase A.
En este caso la respuesta sería la siguiente:
= 0.3 ⋅ 0.1 / 0.5
= 0.06
Sin embargo, a veces podemos tener problemas usando el Teorema de Bayes para clasificar datos que necesita de datos que no tenemos. Dado un punto x, no sabemos la probabilidad de que un punto como x sea tomado como P(X = x), la probabilidad de que un punto aleatorio este en cierta clase como k como P(k) o la posibilidad de que un punto x esté en la clase k: P(X = x|k).
Aún así y con nuestra suposiciones en las distribución de puntos y sus desviaciones estándard, sería posible tener una buena estimación de estos valores.
El primer paso es estimar la posibilildad de que un punto aleatorio este en una clase. Para la clase k, esto se escribe así: πk. Asumiremos que las proporciones de cada clase entre los puntos en el data set será relativamente constante con los puntos nuevos que encontremos.
Ahora, necesitamos calcular la probabilidad de densidad para los puntos en cada clase. El prerequisito para esto es poder calcular los centros de las distribuciones de cada clase y el promedio de la varianza de todo el set. Al tener k clases podemos calcular sus promedios con μk, pero solo con el valor promedio de la varianza σ². Estamos asumiendo que las varianzas de cada clases son iguales, por lo que solo necesitamos un valor.
Cuando hay múltiples variables predictoras, una matriz de valores de covarianza es necesaria para representar adecuadamente las varianzas de las distribuciones gaussianas. En este caso, lo podemos entender con la varianza de un conjunto de puntos que tanto están alejados de su promedio. Antes de calcular la varianza de estos data points, tenemos que eliminar el promedio con la siguiente formula:
Aquí yi representa la clase de xi. Su valor puede ir de 1 a K. Adicionalmente, nk es el número de data points en la clase k.
Con el promedio de cada clase calculada, es ahora posible calcular la varianza con la siguiente fórmula:
Finalmente, tenemos que tener los valores que necesitamos para calcular la probabilidad que el punto x esté en la clase k.
Sin embargo, tenemos que formalmente definir una distribución gaussiana primero. Con la varianza σ² y un promedio μk que sigue la distribución gaussiana significa que
Adicionalmente, dado que cada punto debe estar una de nuestras clases, P(X = x) es la suma de P(X = x|k) por 1 ≤ k ≤ K y P(k) es igual al πk que hemos calculado antes.
Por ello nuestro teorema se ve así:
Esto nos da la función pk(x) = P(k|X = x) que nos indica que nuestra certeza de que el punto x está en la clase k. Si los puntos en nuestro data set tienen una varianza constante y siguen perfectamente distribuciones gaussianas, esta probabilidad está cerca a nuestra mejor estimación. Sin embargo, esta función es muy precica aún con las limitaciones de la vida real. Especialmente cuando hay más de dos clases, tiene un desempeño mejor que la regresión logística.
Por ejemplo, si tenemos n cantidad de puntos y dos clases, un data point x = μ1 con el que calculamos P(X = x) = 0.28 usando el análisis de discriminación linear. Podemos usarlo para calcular el 50% de posbilidades para que x esté en la clase 1 y encontrar que σ² = 1. Esto significaría que:
π1 = √2π ⋅ (0.5 ⋅ 0.28) = 0.35
La clasificación lineal no es el único tipo de algoritmo de clasificación. Existen varias alternativas no-lineales, de las cuales la clasificación del vecino k más cercano (KNN por sus siglas en inglés) es la más simple.
Para usar esta técnica de un punto dado x, empezamos identificandos los puntos k más cercanos a x en el data set. Después clasificamos a x a cualquier clase que se muestre más frecuentemente de estos puntos k. Esta sería un ejemplo de clasificación con k=6.
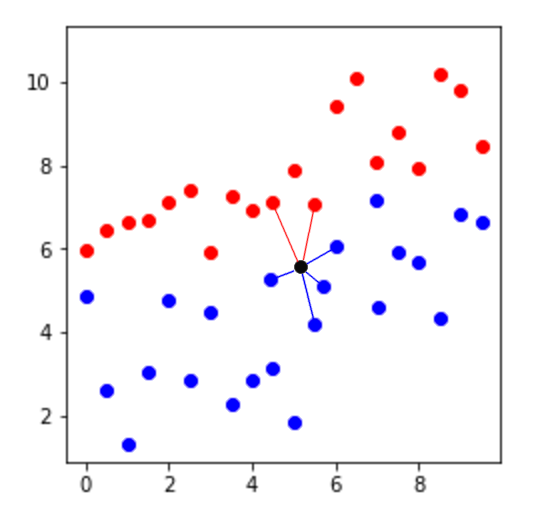
Sin embargo, puede haber un problema como el siguiente:
El punto negro sería clasificado como rojo porque de los 7 puntos más cercanos, 5 son rojos. Aún cuando parece que se ubica en territorio de puntos azules. Lo anterior se debe a la diferencia en la densidad de clases. Si una clase es muy común y la otra es rara, la clasificación KNN tendrá un sesgo hacía la popular.
Una solución común es dar pesos a los data points por el inverso de su distancia desde el punto que está siendo clasificado. Esto significa, dar a los puntos más alejados menos importancia de voto cuando se determina si un punto pertenece a una clase.
Para que KNN sea efectivo, la densidad de puntos en un data set debe alcanzar cierto nivel alrededor de un punto siendo clasificado. Si intentamos clasificar un punto en una area vacía, tomaremos nuestra decisión basada en los data points que estan más alejados de nuestro punto de interés y tendremos resultados inútiles.
Si nuestro data set y los puntos que nos interesan clasificar están hechos de variables predictoras que siempre están entre 0 y 15, estas se encuentran siempre contenidos en un n cubo con una longitud lateral de 15. Si queremos que 15 puntos alcancen una densidad requerida donde solo hay una variable predictora, la cantidad de puntos que necesitamos para un número n de variables predictoras es 15 a la n.
La razón es que nuestro volumen cambia a medida que la dimnesionalidad incrementa. En una dimensión, el volumen es solo el tamaño de una línea. Entonces tenemos solo una variable predictora en donde la densidad es 15/15 = 1 dado que hay 15 puntos en una línea de tamaño 15. Sin embargo, si tenemos dos variables predictoras, los data points están en un cuadrado de volumen 15² = 255. La densidad sería 15/225 con solo 15 data points. Para la densidad anterior, necesitamos 15² = 225 puntos. Este patrón funciona para altas dimensionalidades, en donde n dimensiones permite mantener el mismo promedio de densidad.
En los enfoques anteriores nos hemos concentrado en estimar la probabilidad de que ciertos puntos son parte de ciertas clases. Tanto la clasificación logística como el análisis de discriminación linear funcionan de esta manera.
Sin embargo, no hay ninguna regla que demande encontrar líneas limite. Todo lo que necesitamos son divisiones lineares que separa correctamente las clases y una función que resulte cierta en un lado del divisor y falsa en el otro.
A esta función generalizadora se le conoce como un perceptrón. Se puede resumir como dos partes, un vector de pesos w y un sesgos b. La clase que un perceptrón elige para un punto depende de si las variables predictoras ponderadas del punto superan el sesgo.
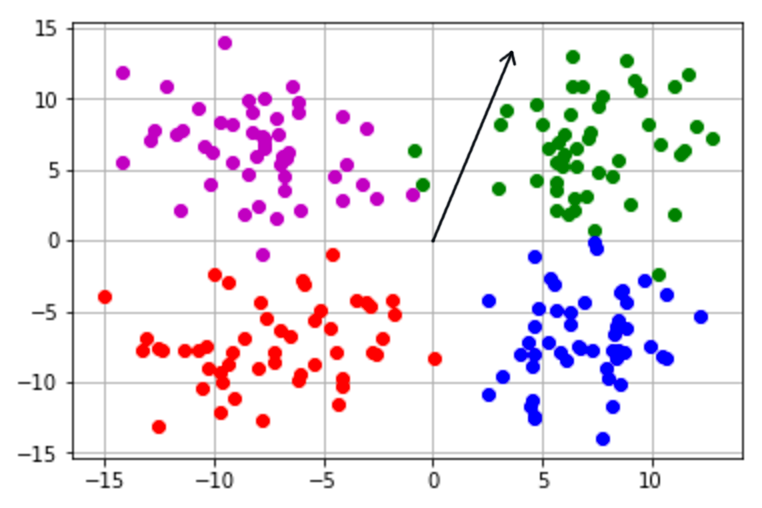
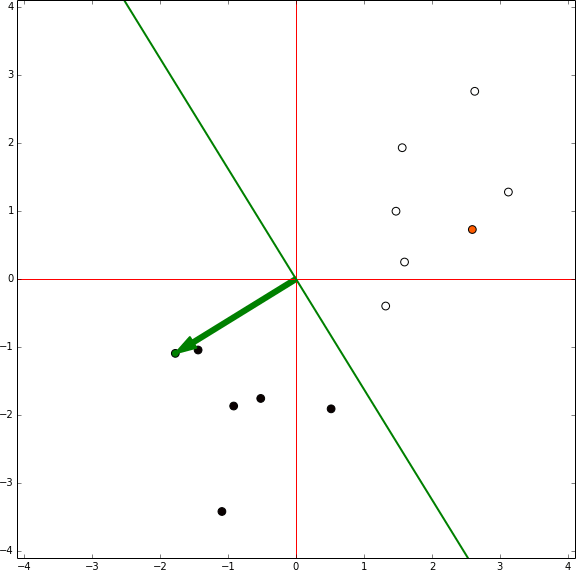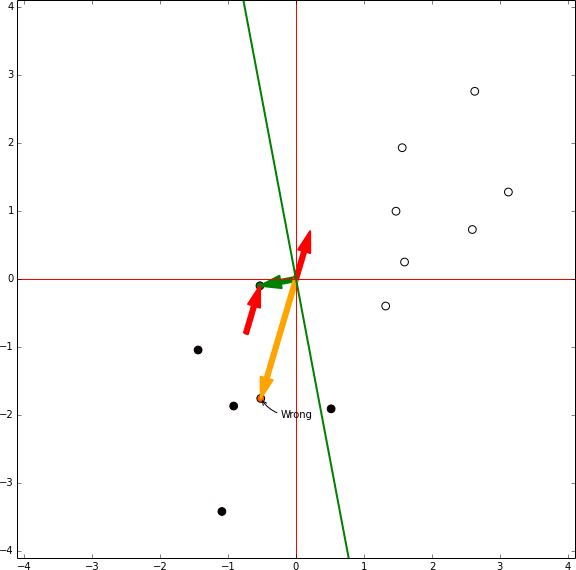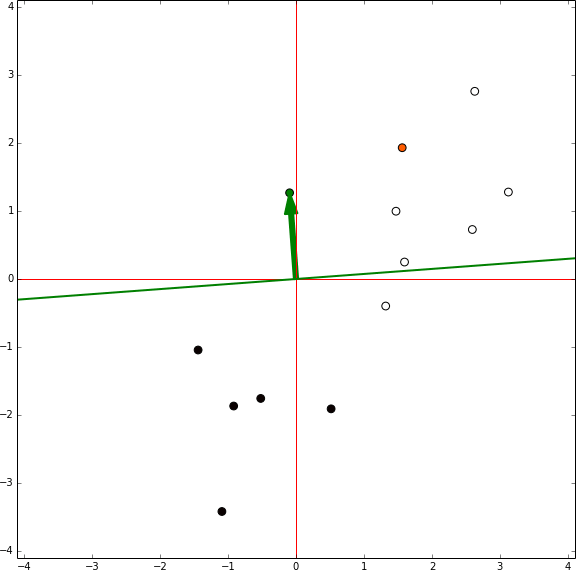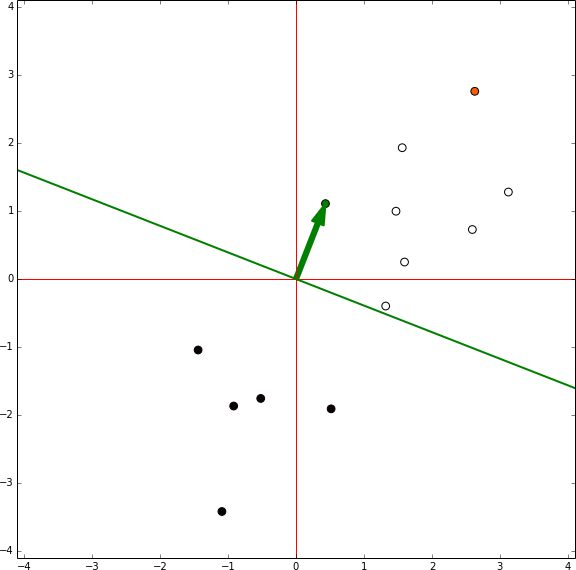
Por ejemplo, dado w y b, un pereceptrón resulta en 1 para una entrada x solo si w ⋅ x ≥ b. De otra manera el resultado es 0. Con estos dos resultados podemos distinguir entre dos clases. En la siguiente imagen tenemos a un vector de peso para un perceptrón, así como cuatro grupos de puntos.
En este caso, los puntos de clase verde nos darían resultados positivos si el perceptrón del sesgo es cero. Podemos ver que el vector de peso apunta hacía arriba y a la derecha del plano. Una de las propiedades del producto punto es que solo puede ser positivo cuando ambos vectores están a menos de 90° de cada uno. Por consecuencia, el grupo verde es enteramente una clase positiva dado que todos los puntos están a menos de 90° de w.
En el proceso de entrenar a un perceptrón, debemos corregir frecuentemente los pesos para lidiar con puntos mal clasificados. Por ejemplo, digamos que tenemos dos clases: azul y roja. Supongamos que nuestro perceptrón verá resultados positivos como rojos y negativos como azúl. Generalmente, si un punto x es mal clasificado como azul debemos de ajustar los pesos del vector w añadiendo x a este. En este caso, podríamos resovlerlo con la siguiente ecuación: (w + x) ⋅ x ≥ w ⋅ x
Una de las propiedades del producto punto es que x + x es igual o mayor que 0 en todos los vectores x. Por lo que podríamos rescribir la ecuación así: (w + x) ⋅ x = w ⋅ x + x ⋅ x ≥ w ⋅ x
Hemos visto en el último problema que si añadimos x a w, entonces w ⋅ x se vuelve más grande. Lo opuesto es cierto; al sustraer x, podemos ver como decrece w ⋅ x.
El significado de esto es que nos permite editar los pesos del vector para asegurarnos que tenga un mejor desempeño clasificando cierto punto x. Si w ⋅ ** x** es menos que b cuando debería ser mayor, podemos añadir x a w y podemos estar seguros que es más correcto que la forma anterior. La misma lógica aplica al caso opuesto.
Similarmente, podemos incrementar el sesgo por uno cuando w ⋅ x ≥ b* incorrectamente y decrecer por uno en el caso opuesto.
A través de este proceso, repetido varias veces es siempre posible separar clases que son separables. Solo tenemos que ir entre cada punto de nuestro data set y si nuestro perceptrón se clasifica incorrectamente, añadimos el punto en el vector de ponderación. De esta manera, el perceptrón convergera con una solución tal como vemos en este ejemplo:
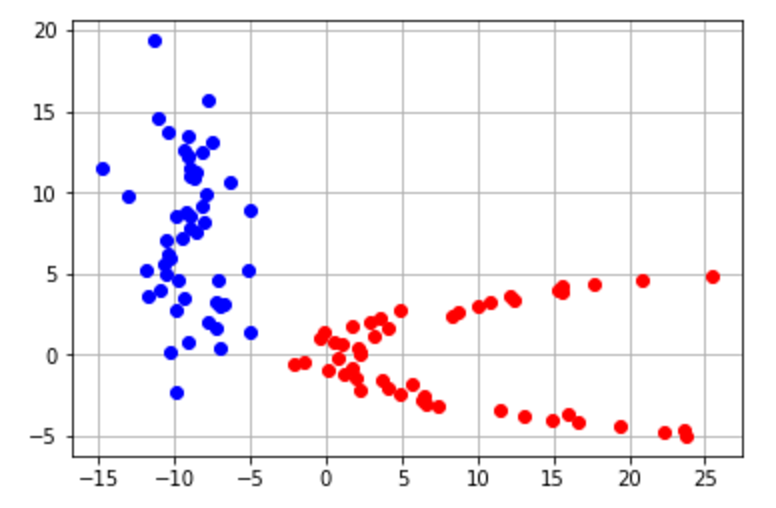
Una forma más entender esto, es si una línea podría ser fácilmente dibujada para dividir dos grupos. Por ejemplo, podríamos crear una línea sencilla que divida los siguientes grupos:
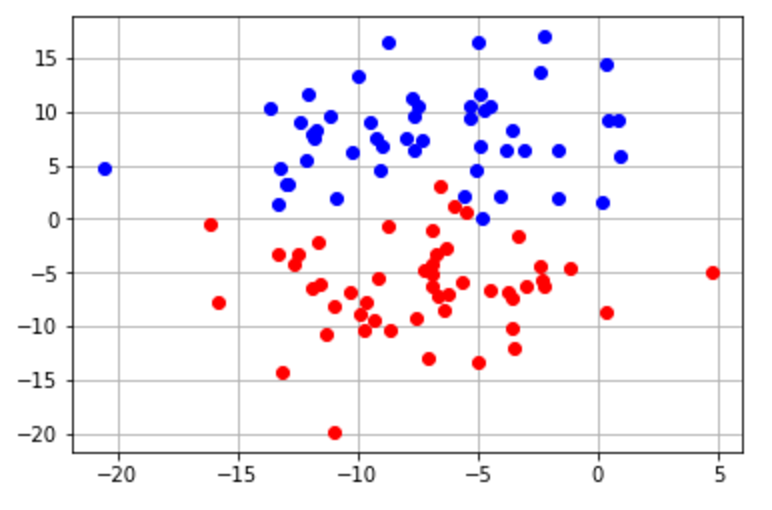
Sin embargo, tendríamos más problema de ubicar una linea en el siguiente gráfico:
El Teorema de Bayes puede ser utilizado para trabajar con variables discretas predictoras que sean valores cualitativos.
Ahora lidearemos con otro modelo clásico de clasificación: Naive Bayes. En este enfoque asumimos que todas las variables predictoras son dependientes de una clase dada (por eso naive de inocente en inglés). Cuando las variables son independientes, es imposible obtener información sobre uno del otro. Por supuesto, las variables predictoras son las únicas que son independientes entre ellas. Aún así, necesitamos predecir el resultado de la variable.
Como cualquier otro clasificador, el objetivo de Naive Bayes es tomar un set de variables predictoras x1, x2, ... xn y regresar una clase basada en sus valores. En este caso, podemos hacerlo al estimar la probabilidad P(k|x1, x2..., xn) por cada clase k.
Podemos entonces ver que usando el teorema de Bayes, tendríamos lo siguiente: P(k|x1, x2..., xn) = P(k|x1, x2..., xn) P(k) / P(k|x1, x2..., xn) dado que las variables asumen ser independientes. Mostramos que P(k|x1,x2,...,xn) = P(x1,x2,...,xn|k)P(k) / P(x1,x2,...,xn).
Naive Bayes también puede servir para trabajar con variables predictoras continuas en vez de cualitativas. Generalmente, esto se hace al asumir que las variables siguen una distribución gaussiana y que estimando la probabilidad de una posición en un punto dado podríamos saber que está en cierta clase usando una función de distribución de probabilidades. La función es dada por estimados de la desviación estándard y el promedio de cada clase.
Lo anterior podría sonar similar al análisis lineal discriminante. Aunque ambas técnicas usan distribuciones gaussianas, el análisis lineal discriminante asume que la desviación estándard de cada clase es la misma. Mientras tanto, Naive Bayes no hace tal suposición por lo que produce resultados diferentes. Sin embargo, estas técnincas son similatres en el caso de una variable si las desviaciones estándard son iguales.