[TOC]
项目要求实现快速排序、枚举排序、归并排序三种排序方法的串行和并行算法,并且进行性能比较和优化分析。其中数据集random.txt,当中包含30000个乱序数据,数据的范围是[-50000,50000],数据间以空格“ ”分隔。
具体要求:
- 用Java多线程或者C#多线程模拟并行处理(推荐用Java)。
- 说明程序执行方式,记录在ReadMe.txt中。
- 读取乱序数据文件
random.txt,排序完成后输出排序文件order\*.txt。(需提交六份order*.txt,命名为order1.txt,order2.txt…以此类推) - 比较各种算法的运行时间,请将运行时间记录在2*3的表格中。行分别表示串行、并行,列分别表示快速排序、枚举排序、归并排序。
- 撰写实验报告,包括并行算法的伪代码、运行时间、技术要点(如性能优化方法)等,结合各自的实验设备(如多核处理器)上的实验结果进行优化,并在实验报告中针对实验结果进行分析(考虑到并行算法多线程在单核处理器中的并行开销,有可能性能会比串行算法下降)。
- 独立完成实验,杜绝抄袭。
function quicksort(L, start, end):
if start < end :
p = partition(L, start, end)
quicksort(L, start, p-1)
quicksort(L, p+1, end)
end if
end functionfunction partition(L, start, end):
pivot = start
i = start;
for j = start to end -1:
if L[j] < pivot:
swap(A[i], A[j])
end if
i = i + 1
end for
swap(A[i], A[end])
return i
end functionfunction RankSort(L, start, end):
for i = start to end:
count = 1
for j= start to end:
if L[i] > L[j] || (L[i] == L[j] && i > j):
x = x + 1;
end if
end for
R[i] = L[i]
end for
end functionfunction MergeSort(L, start, end):
if start < end:
m = (start + end) / 2
MergeSort(L, start, m)
MergeSort(L, m + 1, end)
Merge(L, start, m, end)
end if
end functionfunction Merge(L, start, m, end):
l1 = m - start +1
l2 = end - m
A1 = L[start : m+1]
A2 = L[m+1 : end+1]
i = j = 0
for k = start to end:
if A1[i] < A2[j]:
L[k] = A1[i]
i = i + 1
else:
L[k] = A2[j]
j = j + 1
end if
end for
end functionfunction ParallelQuickSort(L,i, j, m, 0):
if m = 0:
return;
else:
p = partition(L, i, j)
pi send L[p + 1 : j] to pi+1
ParallelQuickSort(L, i, p - 1, m - 1, id)
ParallelQuickSort(L, r + 1, j, m - 1, id + 1)
pi+1 send L[p + 1 : j] to pi
end iffunction ParallelRankSort(L, n):
P0 send L to P1, P2 ...,Pn
for all Pi where 1<= i <= n para-do:
count = 1
for j = 0 to n do:
if L[i] > L[j] || (L[i] == L[j] && i > j):
k = k + 1
end if
end for
end for
P0 merge the result
end functionfunction ParallelMergeSort(L, start, end, k, id = 1):
if start< end :
m = (start + end) / 2
if id + 1 <= m:
Pid+1 do ParallelMergeSort(L, start, m, k, id + 1)
Pid+1 do ParallelMergeSort(L, m + 1, end, k, id + 2)
Set Barrier
Merge(L, start, m, end)
else:
MergeSort(L, start, m)
MergeSort(L, m + 1, end)
Merge(L, start, m, end)
end if
end if
end fucntionJava 具有丰富的多线程机制,可以支持对线程的调度、执行和通信。本次实验主要使用ForkJoinPool维护线程池。
针对多线程并发编程,Java8 当中的 ForkJoinPool可以支持将大任务分解成小任务再并发执行。ForkJoinPool是一种支持任务分解的线程池,当提交给他的任务“过大”,他就会按照预先定义的规则将大任务分解成小任务,多线程并发执行。 一般要配合可分解任务接口ForkJoinTask来使用,ForkJoinTask有两个实现它的抽象类:Recursive Action和Recursive Task,其区别是前者没有返回值,后者有返回值。
下面简单介绍一些在实验当中使用到的Java实现底层的使用方法。
public class ParallelMergeSort<N extends Comparable<N>> extends RecursiveTask<List<N>>
{
@Override
protected List<N> compute(){
if(this.elements.size() <= 1){
return this.elements;
}
else{
final int pivot = this.elements.size() / 2;
ParallelMergeSort<N> leftTask =
new ParallelMergeSort<N>(
this.elements.subList(0, pivot));
ParallelMergeSort<N> rightTask =
new ParallelMergeSort<N>(
this.elements.subList(pivot, this.elements.size()));
leftTask.fork();
rightTask.fork();
List<N> left = leftTask.join();
List<N> right = rightTask.join();
merge(left, right);
return this.elements;
}
}
}在实现ParallelMergeSort的过程当中,我使用了RecursiveTask,通过让ParallelMergeSort继承RecursiveTask实现对多线程的使用,与RecursiveAction不同的是,RecursiveTask有返回值。所以我们可以看见在join时会有返回的List。
public class ParallelQuickSort extends RecursiveAction{
@Override
protected void compute() {
quickSort(elements, start, end);
}
}RecursiveAction与RecursiveTask不同点就在于,它没有返回值。
在双核八处理器的机器上,在保证正确性的条件下,分别进行30次实验,取平均值,可以得到如下耗时比较表格。在比较的过程当中,我还添加比较了Java 自带库当中的Arrays.sort()和Arrays.parallelsort(),以及优化之后使用DoubleMerge算法的并行归并排序。
| 串行 | 并行 | |
|---|---|---|
| Quick Sort | 12.4 ms | 47.4 ms |
| Merge Sort | 16.3 ms | 90.6 ms |
| Rank | 4893.8 ms | 472.7 ms |
| Java Library | 10.0 ms | 17.4 ms |
| DoubleMerge(Parallel) | ---- | 14.2 ms |
从最终实验结果来看,并行条件下,枚举排序的效果比较明显,比在串行条件下的效率提高了90.35% ,并行的提速效果显著。但是我们还是可以看见,快速排序和归并排序的效果并理想,甚至在并行条件下的速度要远低于在串行条件下的速度。
一个可能的解释就是在部分情况下,当单核并行程序转变成并行执行任务时,创建新线程和新任务以及拷贝,等待的通信开销大大超出计算的时间开销。从实验实现的具体底层来看,因为在ForkJoinPool的运行过程中,会创建大量的子任务。而当他们执行完毕之后,会被垃圾回收。这一定程度上导致速度上的下降。
快速排序的速度不够理想,结合具体情况分析,我认为可能是由于以下一些原因。
- 从Java并行实现机制上来讲,使用ForkJoinPool使用过程当中会需要创建大量的子任务,创建子任务的过程会导致效率的降低。事实上,使用ForkJoinPool需要子任务之间相对均衡。但是在quick sort的过程中,子任务的规模不均匀。
- 从数据量的角度来看,当前数据量仅仅为30000,数据量的大小过小导致无法体现并行算法的优越性。
- 快速排序当中的串行分量有点多,像函数
Partition依赖串行实现,效果并不是特别好。
归并排序的速度不够理想,结合具体情况分析,我认为可能是由于以下一些原因。
- 从数据量的角度来看,和快速排序的情况相似,也是数据量的问题,当前数据量仅仅为40000,数据量的大小过小导致无法体现并行算法的优越性。
- 从算法实现来看,在归并排序的实现过程当中,串行分量过多,比如
Merge操作,依赖串行实现,影响了整体的效率。 - 从算法流程上来看,归并排序需要的同步障较多,进程之间相互等待,可能会造成时间上的浪费
- 传统的并行算法,在
Merge的过程当中,每一次merge都会导致增加一半的处理器处于闲置状态,这样就会导致使用效率不高,
针对这些问题,我发现有一个算法DoubleMerge可以解决。这个算法的主要特点就是每个合并操作可以由两个线程同时执行。一个线程可以重复获得两个排序子数组的最小值。直到它合并了一半的元素。另一个线程可以重复获取最多两个已排序的子数组。直到它合并另一半元素。DoubleMerge可以见下图理解。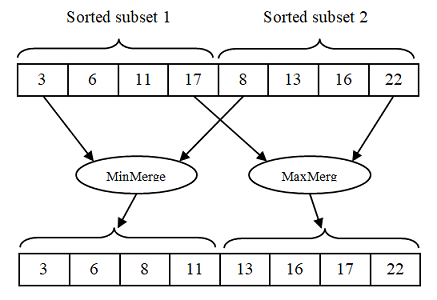
双线程同时执行合并时,它们需要相互等待。其中等待算法如下。
Merging starts{
Merge:
Thread 1: merge mins
Thread 2: merge maxes
Synchronize:
Two threads wait each other
Copy back:
Thread 1: copy back first half
Thread 2: copy back second half
Synchronize:
Two threads wait each other
} Merging ends
该算法性能超过Java自带库并行算法。算法详细细节可以看这一篇论文。
- 枚举排序的并行化转换思路比较清晰,原算法本身通过将每一个元素遍历一遍数组得到合理的位置。这样的流程天生适合并行化的转换。但是受限于排序算法自身设计的缺陷,不能够取得较好的效果。
在一些算法当中可以将一些流程做出改进,比如当子问题规模降低到较小程度时,可以使用简单排序,而不是创建新进程递归。比如在归并排序中,当问题的规模降低到只有32个左右时,可以采用简单快速排序,提高效率。
与思路一相似,在实际操作实现并行排序当中,可以借鉴Java Library库当中的Parallel实现,首先判断问题的规模。如果规模较小,可以直接串行排序;规模较大的情况下,可以使用并行排序。
####思路三
就如同DoubleMerge算法,我们在发现现有并行算法当中串行量太多时,需要根据性能加速比公式,减少串行分量。而减少串行的分量的一个清晰的想法就是,将串行分量转化成并行分量,好比将MergeSort当中的Merge转化成并行分量一样,我们也可以尝试将Quick Sort当中的Partition函数做并行化处理,一样可以获得较好的效果。
在我们现有的多线程体系当中,所有线程的优先级都是一样的,我们可以建立起线程的优先级,建立线程树,让一些线程得到较高的优先级,优先处理。当然了,这就已经不是本次实践考虑的了。
实验本身并不复杂,课堂介绍过详细的实现流程,所以实验的操作难度并不大。但是我还是有一些建议。
-
实验数据可以不要求使用一样的数据, 应该支持使用自身创建的数据。
这样一来,可以设计出较大规模的数据集,使得充分体现并行算法的优越性,同时在设计数据集的过程当中,二来也可以体会到不同倾向的数据适合什么样的排序算法。
-
实验语言可以适当的放宽,在我的实现过程当中,我一度想要使用GPU进行排序,但是考虑到不同语言对CUDA的支持不一样,同时没有支持使用C++,我放弃了这个想法。