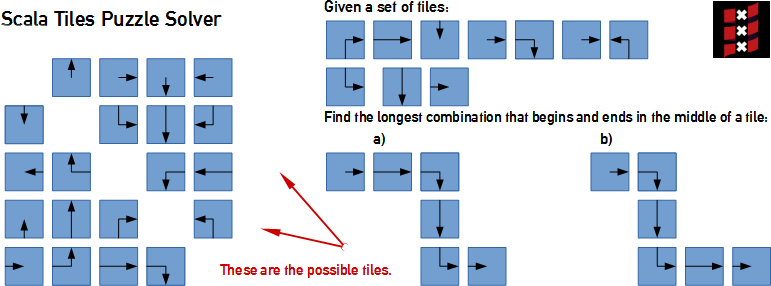
This program solves the puzzle described by the image below.
See this video for the completed application in action.
On a tile there is a directed path which can described as an incoming or start-side and an outgoing or end-side. Each has two of this sides which are named to the cardinal directions. The four directions are denoted with N, E, S, W with the shorthand of the four cardinal directions. If a tile is a beginning (no incoming connection) or an ending (no outgoing connection) then it is denoted with C (for beginning respectively ending in the center aka middle).
We define the matching function between the ends of two tiles with the isJoinable test function (in Scala it could also be seen as an operator). An outgoing ending can be connected with the counter direction of the incoming ending of the other tile. E.g. N with S, W with E and theoretical vice-versa. The C "ending" cannot be connected with any other tile. The ending side is taken in account with the start, so ending side N matches with S and so on.
The solver uses recursive calls. We maintain the list of unused tiles, and we maintain a path. The returning list of the solver method is a list of complete paths, which have proper starting and ending tiles.
The solver filters those tiles in the input list which are prependable to the current path. For each prependable candidate, we call the solver recursively so that the selected tile is prepended to the path and removed form the list of unused tiles.
A solution is generated and appended to the list of returning paths if the selected tile is a beginning tile.
The given 10 tiles which are depicted on the diagram can be noted as:
Tile(N, E), Tile(N, S), Tile(W, C)```
This results in a solution of two list:
```List(Tile(C,E), Tile(W,S), Tile(N,S), Tile(N,E), Tile(W,E), Tile(W,C))``` and
```List(Tile(C,E), Tile(W,E), Tile(W,S), Tile(N,S), Tile(N,E), Tile(W,C))```
# Overlaps
The algorithm simply makes matches with the available unused tiles and takes not in account that some positions are multiple visited. In fact when solutions are generated, the positions of the tiles is directed by the sequence of the tiles.
When we lists that sequence the previous tile will direct the position of the next. E.g. ```Tile(C, E)``` is the cause of it that the next tile is east of this tile. This is indicated by a red border in the GUI (graphical user interface). With a checkbox checked the mostly more than one solutions will be filtered and the solutions with multiple tiles on one position will be taken out and not be presented in the GUI.
# Hints & Kinks
- The algorithm starts with one of the **ending tiles**, this is done for the nature of List prepending is computational cheaper than appending.
- we used high order *combinators* (```filter()```, ```distinct```, etc.) to implement the solver's algorithm
- Although we have to use Set, the use is postponed by using List because a Set has overhead to enforce uniqueness.
- Removing one element in List is easily made with the ```diff List(elem)```
## Contributing / Issues
Please post any issues or ideas you have to [Tiles puzzle solver's issues](https://github.com/amsterdam-scala/AS-Tiles-puzzle-solver/issues)
If you like rolling up your sleeves, feel free to fork and create a feature branch.

The solver solvers @ April 17, 2014
---