RedesDePetri
Las Redes de Petri (RdP), también conocidas como Redes de Petri Ordinarias, conforman una herramienta gráfica y matemática útiles para el modelado de sistemas.
Una RdP ayuda a mostrar información muy valiosa respecto a la estructura del sistema modelado como así también del comportamiento dinámico de dicho sistema modelado.
Gráficamente una RdP es un grafo. Un grafo es una interconexión de nodos. En las RdP se interconectan dos tipos de nodos, sus plazas (círculos) y sus transiciones (rectángulos negros). De esta forma las RdP se componen de 4 elementos principales, estos son:
- Plazas
- Transiciones
- Tokens
- Arcos
Plazas
Las plazas gráficamente son representadas por círculos blancos como muestra la imagen.
Dentro del modelado de sistemas las plazas representan por lo general dos características diferentes, estas son:
- Estados de un proceso involucrado en el sistema modelado.
- Recursos que se involucran en el sistema modelado.
Transiciones
Las transiciones gráficamente son representadas por rectángulos negros de acuerdo con la imagen.
Tokens
Los tokens en su conjunto indican el estado actual en el que se encuentra el sistema modelado.
Arcos
Las plazas gráficamente son representadas por cada una de las flechas que interconecta los diferentes tipos de nodos de la red.
Cada uno de los arcos representan las diferentes relaciones existentes entre un estados de procesos, recursos y acciones que pueden realizar los procesos en dichos estados.
Sistema real vs Modelado de sistema (RdP)
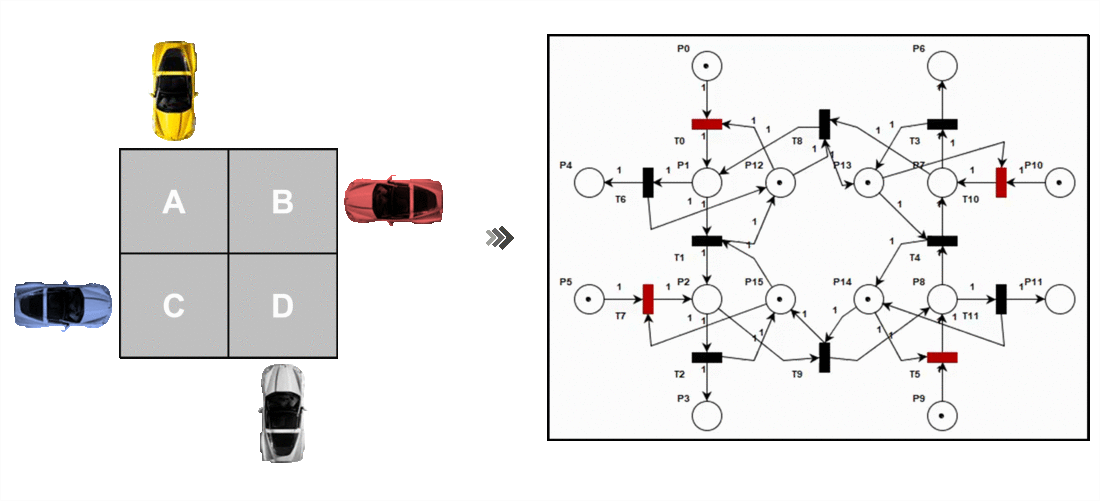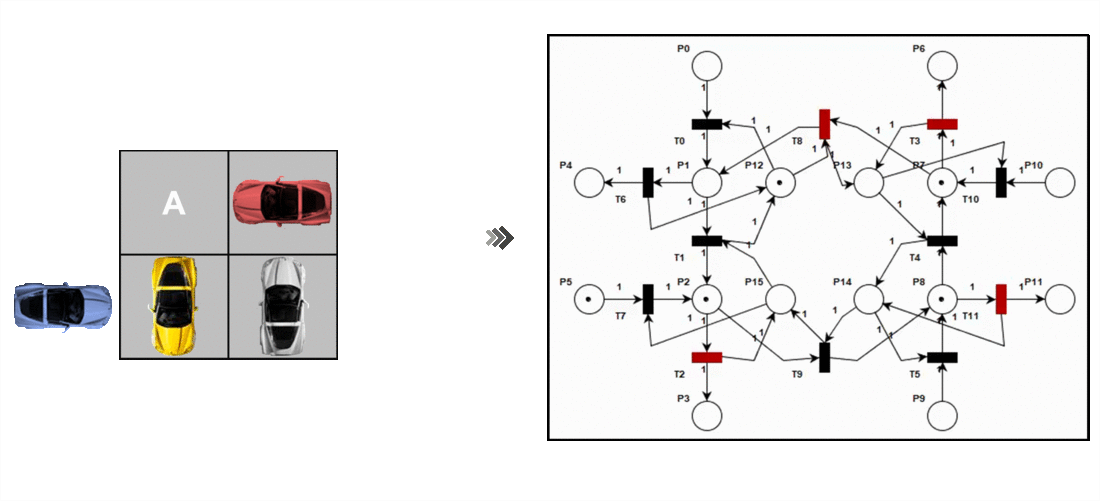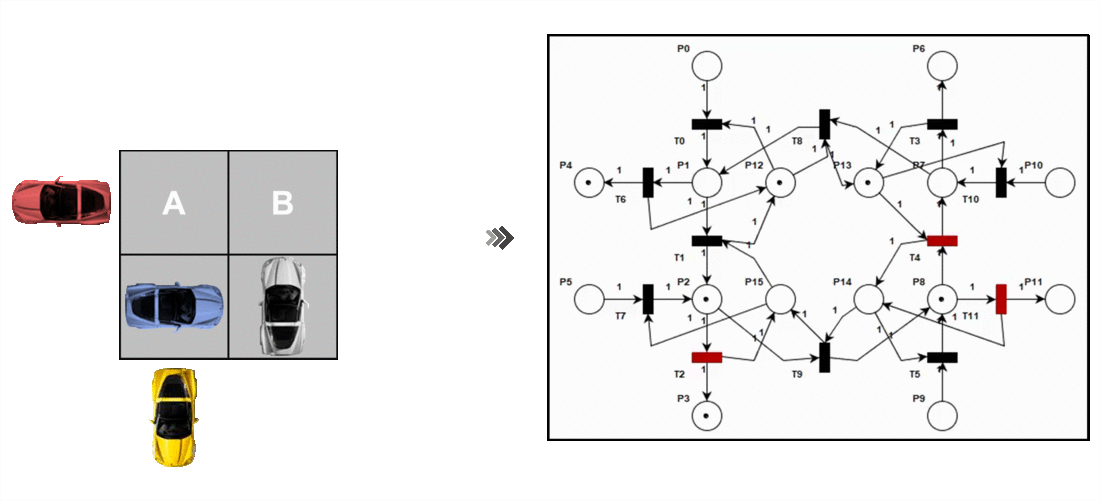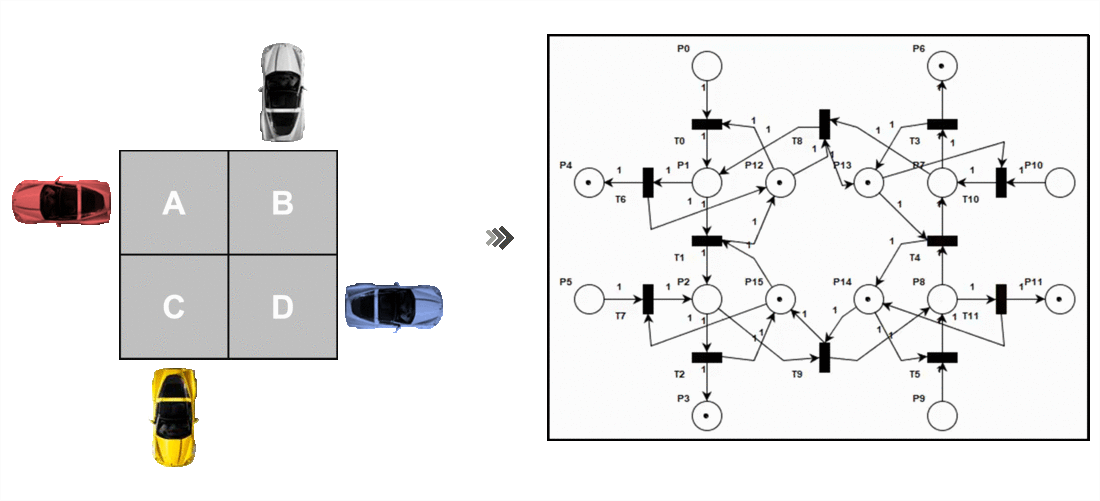
La mayor importancia de estas redes es que poseen un modelo matemático simple, potente y altamente aplicable a cualquier sistema de computación. A su vez el modelo matemático sirve como base para la evolución a otros tipos de redes de mayor semántica como lo son las Redes de Petri Generalizadas.
Las RdP pueden aplicarse a cualquier sistema de computación ya que poseen un modelo matemático altamente aplicable a estos, incorporándose como un conjunto de software o firmware. Por esta ultima razón las RdP se pueden aplicar en sistemas de propósito general, sistemas embebidos o sistemas de tiempo real.
En computación, las RdP abarcan una gran variedad de areas de aplicación, algunas de ellas son:
- Análisis de datos.
- Diseño de software.
- Fiabilidad.
- Flujo de trabajo.
- Programación concurrente (control de subprocesos).
Por ejemplo en el presente proyecto se las utilizo como una solución ideal para los sistemas paralelos que requieran simulación y modelado de la concurrencia en los recursos compartidos por subprocesos del sistema operativo Linux controlados desde Device Driver Linux MatrixmodG.