Given an m x n board of characters and a list of strings words, return all words on the board.
Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.
Example 1:
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]
Example 2:
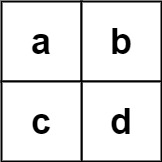
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []
Constraints:
m == board.lengthn == board[i].length1 <= m, n <= 12board[i][j]is a lowercase English letter.1 <= words.length <= 3*10^41 <= words[i].length <= 10words[i]consists of lowercase English letters.- All the strings of
wordsare unique.
題目給定一個 m by n 字元矩陣 board 還有一個字串 array words
要求實作一個演算法找出字串 array words 有哪些字串存在於 m by n 矩陣
在 m by n 矩陣搜詢一個字串做的法是從每個字元當作起點針對上下左右四個方向做 DFS 找尋有可能的字串,所以最遭的狀況就是
Trie 的結構能夠有效讓要搜尋的字串可以用一個很有效率的方式做比對
如下圖
import java.util.ArrayList;
import java.util.HashMap;
import java.util.HashSet;
import java.util.List;
public class Solution {
static class Node {
HashMap<Character, Node> Children = new HashMap<>();
boolean isWord = false;
String Word = "";
}
static class Trie {
Node root;
Trie() {
root = new Node();
}
public void addWord(String word) {
Node cur = root;
int size = word.length();
for (int pos = 0; pos < size; pos++) {
char ch = word.charAt(pos);
if (!cur.Children.containsKey(ch)) {
cur.Children.put(ch, new Node());
}
cur = cur.Children.get(ch);
}
cur.isWord = true;
cur.Word = word;
}
}
int ROW, COL;
public List<String> findWords(char[][] board, String[] words) {
ROW = board.length;
COL = board[0].length;
boolean[][] visit = new boolean[ROW][COL];
HashSet<String> hashSet = new HashSet<>();
Trie trie = new Trie();
for (String word : words) {
trie.addWord(word);
}
for (int row = 0; row < ROW; row++) {
for (int col = 0; col < COL; col++) {
DFS(row, col, trie.root, visit, board, hashSet, words.length);
}
}
return new ArrayList<>(hashSet);
}
public void DFS(int row, int col, Node node, boolean[][] visit,
char[][] board, HashSet<String> hashSet, int max) {
Node cur = node;
if (row < 0 || row >= ROW || col < 0 || col >= COL) {
return;
}
if (visit[row][col]) {
return;
}
char ch = board[row][col];
if (!cur.Children.containsKey(ch)) {
return;
}
visit[row][col] = true;
cur = cur.Children.get(ch);
if (cur.isWord) {
hashSet.add(cur.Word);
}
if (hashSet.size() == max) {
return;
}
DFS(row-1, col, cur, visit, board, hashSet, max);
DFS(row+1, col, cur, visit, board, hashSet, max);
DFS(row, col-1, cur, visit, board, hashSet, max);
DFS(row, col+1, cur, visit, board, hashSet, max);
visit[row][col] = false;
}
}- 理解使用 DFS 針對 4個方向去找可能的值
- 理解透過 Tries 來減少搜尋的次數,透過 Trie 結構可以一次找到多個 prefix 一樣的字串
- Understand what problem need to solve
- Analysis complexity