-
Notifications
You must be signed in to change notification settings - Fork 46
PyTMatrix Kdp example
Jussi Leinonen edited this page Jan 8, 2014
·
1 revision
The code given below produces the following plot using PyTMatrix:
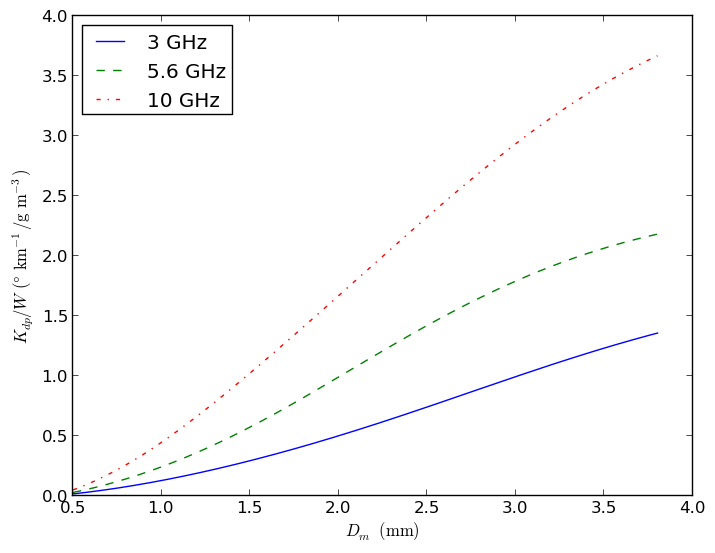
See also the examples on the main wiki page.
#!/usr/bin/env python
"""
This demo replicates Fig. 7.7 from Bringi and Chandrasekar (2001),
Polarimetric Weather Radar: Principles and Applications. It shows the
specific differential phase (Kdp) normalized by the total water content (W)
as a function of the mass-weighted mean diameter.
"""
from matplotlib import pyplot as plt
import numpy as np
from scipy import constants
from pytmatrix.tmatrix import Scatterer
from pytmatrix import psd, orientation, radar, tmatrix_aux
# define an exponential psd (eq. 7.12 with mu=0)
class ExponentialPSD(object):
def __init__(self, lam=1.0, N0=1.0):
self.lam = float(lam)
self.N0 = float(N0)
def __call__(self, D):
return self.N0*np.exp(-self.lam*D)
# the Beard-Chuang axis ratio (eq. 7.3)
def axis_ratio(D):
return 1.0/(1.0048 + 5.7e-4*D - 2.628e-2*D**2 + 3.682e-3*D**3 -
1.677e-4*D**4)
# initialize a scatterer object
scatterer = Scatterer()
scatterer.set_geometry(tmatrix_aux.geom_horiz_forw)
# set up orientation averaging, Gaussian PDF with mean=0 and std=7 deg
scatterer.or_pdf = orientation.gaussian_pdf(7.0) # orientation PDF
scatterer.orient = orientation.orient_averaged_fixed # averaging method
# set up PSD integration
scatterer.psd_integrator = psd.PSDIntegrator()
scatterer.psd_integrator.D_max = 8.0 # maximum diameter considered
scatterer.psd_integrator.geometries = (tmatrix_aux.geom_horiz_forw,)
scatterer.psd_integrator.axis_ratio_func = axis_ratio
Dm = np.linspace(0.5, 3.8, 1000) # range of Dm (mm)
lam = 4.0/Dm # corresponding lambda parameters
W = np.pi*1e3*(Dm/4.0)**4 # corresponding water content
wavelengths = constants.c/np.array([3e9, 5.6e9, 10e9]) * 1e3 # in mm
ref_indices = [complex(8.983, 0.989), complex(8.590, 1.670),
complex(7.718, 2.473)]
labels = ["3 GHz", "5.6 GHz", "10 GHz"]
styles = ["-", "--", "-."]
# this calculates Kdp for the given lambda parameter
def get_Kdp(lam):
scatterer.psd = ExponentialPSD(lam=lam) # set exponential PSD
return radar.Kdp(scatterer)
plt.figure()
for (wl, m, label, style) in zip(wavelengths, ref_indices, labels, styles):
scatterer.wavelength = wl
scatterer.m = m
# initialize lookup table
scatterer.psd_integrator.init_scatter_table(scatterer)
Kdp = np.array([get_Kdp(l) for l in lam])
plt.plot(Dm, 1e6*Kdp/W, ls=style, label=label) # 1e6 for unit conversion
plt.xlabel(r"$D_m$ $\mathrm{(mm)}$")
plt.ylabel(r"$K_{dp}/W$ $\mathrm{(\degree \, km^{-1} / g \, m^{-3})}$")
plt.legend(loc='best')