golang_swim_in_rising_water

You are given an n x n integer matrix grid where each value grid[i][j] represents the elevation at that point (i, j).

The rain starts to fall. At time t, the depth of the water everywhere is t. You can swim from a square to another 4-directionally adjacent square if and only if the elevation of both squares individually are at most t. You can swim infinite distances in zero time. Of course, you must stay within the boundaries of the grid during your swim.

Return the least time until you can reach the bottom right square (n - 1, n - 1) if you start at the top left square (0, 0).

Examples

Example 1:

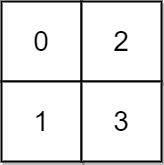
Input: grid = [[0,2],[1,3]]
Output: 3
Explanation:
At time 0, you are in grid location (0, 0).
You cannot go anywhere else because 4-directionally adjacent neighbors have a higher elevation than t = 0.
You cannot reach point (1, 1) until time 3.
When the depth of water is 3, we can swim anywhere inside the grid.

Example 2:

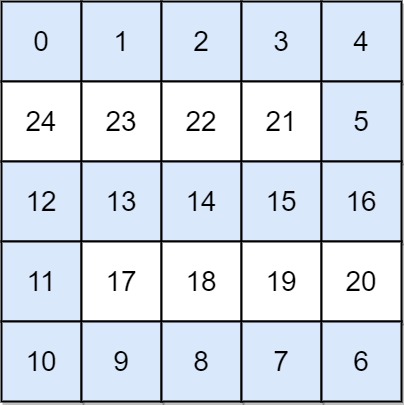
Input: grid = [[0,1,2,3,4],[24,23,22,21,5],[12,13,14,15,16],[11,17,18,19,20],[10,9,8,7,6]]
Output: 16
Explanation: The final route is shown.
We need to wait until time 16 so that (0, 0) and (4, 4) are connected.

Constraints:

• n == grid.length
• n == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] < n2
• Each value grid[i][j] is unique.

解析

題目給定一個整數矩陣 grid ，其中每個 entry, grid[r][c] 代表該 cell 的高度

假設要經過時間 t , 水才會注滿到 t 單位高度 ，代表在時間 t 時， 可以到達 grid[r][c] ≤ t 的相鄰 cell

要求寫出一個演算法計算從 row = 0, col = 0 開始出發達到 row = N-1, col = N-1 最小需要花多少時間

這題的關鍵在於每個 grid[r][t] 到表該 cell 要到達至少需要多少時間

而每次要需要當下 cell 的時間與之前 cell 時間取最大值這樣才能確保能從之前的 cell 到達這個 cell

透過這樣資訊還有 grid 每個 cell 的水平與垂直相對結構

使用 Dijkstra's algorithm

也就是透過 MinHeap 做 BFS 當走到 row = N - 1 , col = N - 1 所累計的時間就是答案

如下圖

程式碼

package sol

import "container/heap"

type Pair struct {
	Row, Col int
}
type AdjacentNode struct {
	Time  int
	Coord Pair
}
type AdjacentMinHeap []AdjacentNode

func (h *AdjacentMinHeap) Len() int {
	return len(*h)
}
func (h *AdjacentMinHeap) Less(i, j int) bool {
	return (*h)[i].Time < (*h)[j].Time
}
func (h *AdjacentMinHeap) Swap(i, j int) {
	(*h)[i], (*h)[j] = (*h)[j], (*h)[i]
}
func (h *AdjacentMinHeap) Push(value interface{}) {
	*h = append(*h, value.(AdjacentNode))
}
func (h *AdjacentMinHeap) Pop() interface{} {
	old := *h
	n := len(old)
	x := old[n-1]
	*h = old[0 : n-1]
	return x
}
func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}
func swimInWater(grid [][]int) int {
	N := len(grid)
	visit := make(map[Pair]struct{})
	directions := []Pair{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}
	priorityQueue := &AdjacentMinHeap{AdjacentNode{Time: grid[0][0], Coord: Pair{Row: 0, Col: 0}}}
	heap.Init(priorityQueue)
	for priorityQueue.Len() != 0 {
		node := heap.Pop(priorityQueue).(AdjacentNode)
		if node.Coord.Row == N-1 && node.Coord.Col == N-1 {
			return node.Time
		}
		for _, direction := range directions {
			shiftedRow := node.Coord.Row + direction.Row
			shiftedCol := node.Coord.Col + direction.Col
			if _, ok := visit[Pair{Row: shiftedRow, Col: shiftedCol}]; shiftedRow < 0 || shiftedRow == N || shiftedCol < 0 || shiftedCol == N || ok {
				continue
			}
			visit[Pair{Row: shiftedRow, Col: shiftedCol}] = struct{}{}
			heap.Push(priorityQueue,
				AdjacentNode{Time: max(node.Time, grid[shiftedRow][shiftedCol]),
					Coord: Pair{Row: shiftedRow, Col: shiftedCol}})
		}
	}
	return 0
}

困難點

1. 要理解每個 grid[r][c] 與時間的關係
2. 理解 Dijkstra's algorithm

Solve Point

• 透過 grid[r][c] 把每個座標對應可到達最小時間放到 priorityQueue 中
• 透過 HashTable 紀錄已經拜訪過的 vertex 避免重複拜訪
• 每次放入的時間都取 max(grid[r][c], 上一個到達時間)