-
Notifications
You must be signed in to change notification settings - Fork 53
Sommer Sitzung 04
Fabian Steeg edited this page Jun 20, 2011
·
1 revision
| Thema | Stichworte | Material ___________________________ |
| Überblick | Heute wieder Datenstrukturen: Bäume – eine vielseitige Datenstruktur | Beispiele und Literatur: Home |
| Bäume als Struktur | — | — |
| 1. Grundlagen | Warum flexibel? – Woher Bäume als Struktur bekannt? – z.B. Stammbaum; allgemeiner? – für hierarchische Strukturen (Arten von X), Teil-Ganzes-Beziehung (Teile von X), etc.; konkret? – Dateisystem, Wissen (z.B. Struktur dieser Sitzung, Tierreich, etc. – vgl. Wikipedia); Blätter, innere Knoten; Root/Wurzel; Vorfahre, Nachfahre/Child, Geschwister/Sibling |   |
| 2. Details und Rekursion | Formale Definition: Graph allgemein? – Knoten (Informationsspeicher, enthält einen Wert), Kanten, z.B.? – UML-Diagramme; Baum vs. Graph? – bei Baum jeder Knoten von Wurzel aus erreichbar (DAG); Baum vs. DAG? – Baum ist DAG mit 1 Vorgänger pro Knoten, ausser Root; Woraus besteht ein Baum? – Baum rekursiv: ein Baum ist leer oder enthält weitere Teilbäume; Grad eines Knotens: Anzahl seiner direkten Nachfolger, z.B. 2: Binärbäume; Stufe/Level: Wurzel 1, jeder Nachfolger 1 mehr; Höhe/Tiefe: max. Stufe | 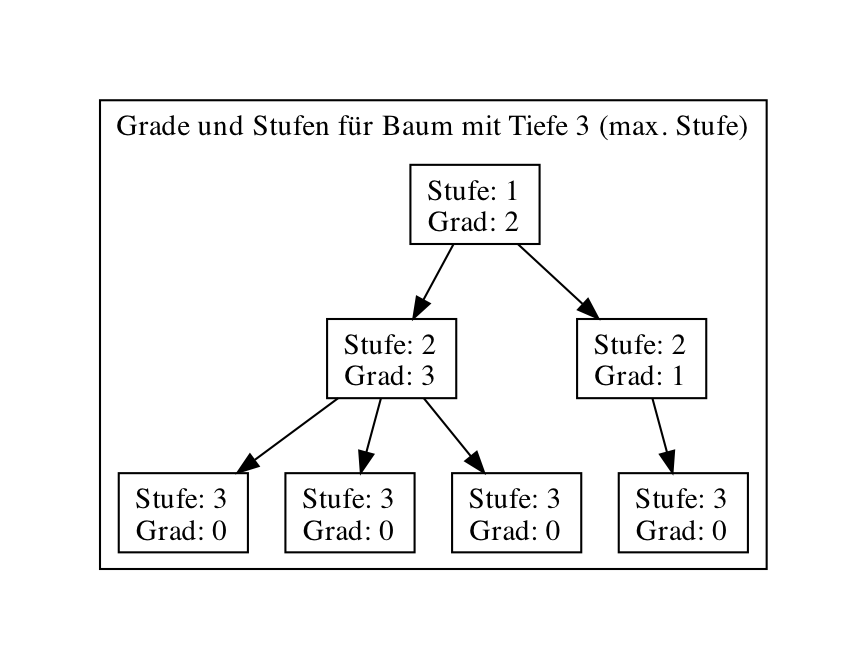 |
| 3. Operationen auf Bäumen | Was machen wir mit so einem Baum? – Suchen nach Wert, Suchen nach Pfad (z.B. Dateisystem); Traversieren (Durchlaufen), wozu? – z.B. zur Ausgabe, oder mit allen was machen, vgl. Iterator; Einfügen; Löschen; d.h. wir haben flexible Möglichkeiten zur Arbeit einer strukturierten Informationsbasis (abfragen, verarbeiten, verwalten) | — |
| Binäre Suchbäume | — | — |
| 1. Binäre Suchbäume: Konzept | Anwendung von Bäumen für Suchproblem; wie ging binäre Suche? – Gemeinsamkeit mit binärer Suche? – binäre Suche lässt sich als Baum darstellen, jeweils Mitte nächster Knoten, immer links oder rechts weiter; links immer Werte die kleiner sind, rechts >= als aktueller Knoten; Bsp. Aufbau und Suche; bei Suche einfach ab Wurzel zum gesuchten Element durchlaufen; welche Eigenschaft von Bäumen nutzen wir hier aus? – Jeder Knoten wird von Wurzel erreicht; ist das Baum-spezifisch? – DAG; wie schon vorher: Prinzip gleich auch für komplexe Objekte (Bücher, Adressen, Dokumente, etc.) |  Einfügen für Einfügen für 5,3,8,2,4,7,6; Beispielsuche konzeptuell |
| 2. Binäre Suchbäume: Laufzeit | Bestenfalls: exakt wie binäre Suche: O(log n); was kann schief gehen? – naiv einfügen: z.B. erstes Wort, dann alle links oder rechts einfügen; wann Problem? – was konnte bei insertion sort schief gehen? – z.B. schon aufsteigend sortiert, was passiert? – immer rechts eingefügt; Effekt? – Baum entartet, Laufzeit wird? – n statt log n; Verhindern? – Baum reorganisieren wenn nötig (AVL- oder Red-Black-Trees); kostet Rechenzeit; lohnt wann? – wenn wir viel mehr suchen als einfügen; klassische Aspekte beim Nachdenken über Algorithmen und Datenstrukturen: Rechenzeit und Speicherplatz, oft abwägen je nach Fall | — |
| 3. Binäre Suchbäume vs. binäre Suche | Warum überhaupt Bäume statt binäre Suche, wenn gleiche Komplexität? – 1.) automatisch immer sortiert, kein Vorsortieren nötig 2.) Lösung über ‘intelligente’ Datenstruktur: statt low-level führe Sortierung durch, dann Suche binär high-level: wir bauen ein Ding, was das kann, das so funktioniert wie wir das brauchen: einfügen, schnell Suchen; und Sortierung implizit, wann? – in bestimmter Weise (In-order, s.u.) traversieren; allgemeiner Ansatz für sauberen Code: elegant, problemnah formulieren; quasi: statt auf einfacher Struktur trickreich abrufen, rufen wir auf trickreicher Struktur einfach ab; je nach Fall, z.B. wenn schon sortiert binäre Suche gut etc.; bisher also konzeptuell Bäume allgemein und binäre Suchbäume speziell | — |
| Implementierung von Bäumen | — | — |
| 1. Baumstruktur | OOP-Ansatz wie bei verk. Listen; wie? – Pointer, Elemente verketten; Unterschied? – Wert und mehrere Pointer, statt ein Pointer wie bei verketteter Liste; Binärbaum: 2, allgemeiner Baum? – Bäume als Listen von Listen; wie konkret? – 1.) children: List (n Referenzen); oder, sparsamer? basierend auf Paar-Idee bei verketteten Listen: 2.) head: Node, tail: Node (2 Referenzen); s. Code |  |
| 2. Baumoperationen | 1.) Einfügen; wie implementieren? – Rekursive Methode für rekursive Struktur, wie? – Suche Einfügeposition je nach Wert im linken oder rechten Teilbaum weiter, bis Baum leer (s. Code); auch iterativ möglich (s. Code); 2.) Abfragen (Hausaufgabe), als Vorbereitung: 3.) Traversieren; für Teilbaum aus drei Knoten welche Alternativen? – 3 Standard-Reihenfolgen, Vorstellung: left u. right fest, root flexibel: Pre-order: root, links, rechts; In-order: links, root, rechts; Post-order: links, rechts, root; wie z.B. In-order implementieren? – z.B. Werte sammeln in Liste, s. Code; Entartung zeigen, was bei diesem naiven Einfügen bei sortierten Daten? – entartet maximal, Alternative? – binäre Suche: schon korrekt vorverarbeitet |  Bsp. Teilbäume traversieren: pre, in, post; s. Code Bsp. Teilbäume traversieren: pre, in, post; s. Code |
| 3. Visualisierung | DOT, eine DSL für Graphen; DOT-Format f. Bäume: digraph{1->2;1->3} (vgl. Begriffe bisher: directed, graph, node, edge); wie erzeugen? – traversiere z.B. inorder, in DOT umwandeln durch rausschreiben in String, dann File: root->left;root->right, s. Code |
Code; Bild-Export (Abb. oben) |
| Hausaufgabe | Traversieren inorder und postorder; Wert in Baum suchen: contains; Graphviz verwenden |
Sommer-Aufgabe-03 |