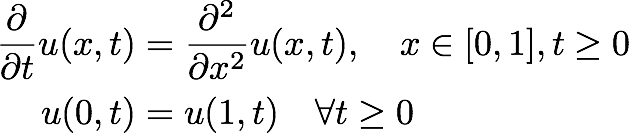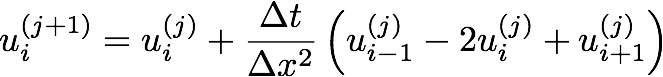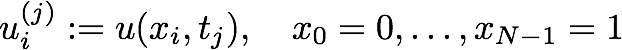In Homework #4 we will solve the heat equation using MPI via a domain decomposition method similar to the technique used in the array shift code from Lecture #15. This assignment will require that you read more code than you will write.
Important: this assignment requires that mpi4py be installed in your
compute environment:
$ pip install mpi4py
Your homework tests will not work until this is installed!
The makefile for this homework assignment has been provided for you. It will
compile the source code located in src/ and create a shared object library
lib/libhomework4.so.
Run,
$ make lib
to create lib/libhomework4.so. This library must exist in order for the Python
wrappers to work. As a shortcut, running
$ make test
will perform the parallel tests:
$ make lib
$ mpiexec -n 3 python test_homework4.py
Important: Read the contents of test_homework4.py to get an idea as to
what is going on when you run mpiexec -n 3 python test_homework4.py after
implementing src/heat.c:heat_parallel(). The observant student will realize
that each process is running it's own version of the test suite. However, only
Process 0 will actually compare the parallel solution to the serial solution.
The test suite test_homework4.py also contains some code for generating plots
of an example heat equation problem using both the serial and the parallel
versions. Usage of these functions are demonstrated within the two provided
plotting functions as well as in the if __name__ == main` block at the
bottom of the test script.
In this assignment we will numerically solve the periodic heat equation
using the Forward Euler method
where
First, read the contents of src/heat.c:heat_serial(). This is a completely
serial implementation of Forward Euler for solving the heat equation. To see
this in action, compile src/heat.c into a shared object library via make lib
and then run the test suite:
$ python test_homework4.py
In particular, make sure that only the plot_example_serial() function is
called when run. (As in the original state of the test script.) This will create
a plot called serial_heat.png in your project directory.
Some key things to observe about heat_serial():
- This function solves the heat equation on input data
urepresenting an initial condition on the whole intervalx \in [0,1]. The input example data is defined intest_homework4.py. - The outmost loop within the function performs the time iteration.
- The inside loop performs Forward Euler on the interior nodes of
utto obtain the interior nodes ofutp1. That is, the loop only computes the iterates:utp1[1], ..., utp1[Nx-2]. - After the inside loop, we separately iterate at the "boundaries". (Quotation
marks used because we're acutally solving the periodic problem so there really
isn't a boundary.) That is, since we're solving the periodic problem the
solution at
utp1[0], for example, uses the data atut[0],ut[1], andut[Nx-1].
Next, read the contents of test_homework4.py. In this homework assignment
the test suite that we will use against your implementation of
src/heat.c:heat_parallel() has been provided to you. See the section "1)
Tests - 60%" below for more information.
Finally, write the requested C/MPI code. Implement the function described
below. (Only one function in this homework.) As usual, homework4/wrappers.py
contains the Python wrappers for the C functions you will be using.
-
src/heat.c:heat_parallel()Much of the boilerplate has been written for you. You will be asked to write the "interesting part" using the appropriate MPI functions. Following the pattern of
shift.cin Lecture #15, writeheat_parallel()such that it behaves in the following way:-
Each process such that each process recieves a "chunk",
double* uk, of the solution vector. Note that, as inshift.c, each process will callheat_parallel()setting its own values forrankandsizeviaMPI_Comm_rank()andMPI_Comm_size(), respectively. These chunks represent parts of the "whole" solution,u. That is, if the whole data arrayuisNelements long then Process 0 receives the firstNxelements ofu, Process 1 receives the nextNxelements, etc., and Processsize-1receives the lastNxelements whereNx = N / size.Here's a picture similar to that in Lecture #15's
shift.cto better explain the situation:Proc0 Proc1 Proc2 [a, b, c] [d, e, f] [g, h, i] *--*---* ^ | computing solution at this point in Proc 0 requires knowing the left-boundary data at Proc 1 "Whole data array": u = [a, b, c, d, e, f, g, h, i] Proc 0: uk = [a, b, c] Proc 1: uk = [d, e, f] Proc 2: uk = [g, h, i] (Computing the solution at `b` using Forward Euler only requires `a`, `b`, and `c` so it can be done without needing to communicate data to other processes.) -
Each process should numerically solve the heat equation within its own chunk, communicating the required boundary data to "adjacent" processes as necessary. Note that the data communication is necessary because computing
uktp1[0]requires knowing the right-boundary value of theutarray belonging to the left process. In other words, computinguktp1[0]at processkrequires the value ofukt[Nx-1]at processk-1. Similar data transfers need to occur at the right boundary,uktp1[Nx-1]of processk. -
Because we wish to solve the periodic heat equation problem, the
rank = 0process needs to communicate its boundary data with therank = size - 1process and vice-versa. (In addition to the necessary boundary communication between processes at rankk-1,k, andk+1for allk.)
-
The wrapper function homework4/wrapper.py:heat_parallel() calls
src/heat.c:heat_parallel(), passing in an MPI_Comm object which is generated
by mpi4py. See the test script for example usage of this wrapper function
within a parallel context.
Because we haven't discussed mpi4py in much detail the test suite that we will
use against your code has been provided to you. Please read the contents of
test_homework4.py. Again, note that the parallel test code is to be executed
via
$ make lib
$ mpiexec -n 3 python test_homework4.py
meaning that each spawned process will be running the test suite on its own. (However, only Process 0 concatenates the parallel results and compares with the serial solution.)
Make sure your implementation of src/heat.c:heat_parallel() causes the test to
pass. You only have one test so make it count!
Some additional functions have been provided to you within test_homework4.py
demonstrating how to, for example, call heat_parallel() and plot the results.
In particular, take a look at the example usage provided to you at the bottom of
the test script:
if __name__ == '__main__':
# plot the serial result to see what kind of initial condition and solution
# is expected.
#
# $ python test_homework4.py
#
# (Comment this out when running parallel tests. See below.)
plot_example_serial(chunks=3, Nt=100)
###################################################
# RUN THE TESTS AND PARALLEL PLOT BELOW USING MPI #
# #
# $ mpiexec -n 3 python test_homework4.py #
# #
# (Comment out the serial plot, above, and remove #
# the comments below to run the tests!) #
###################################################
# plot the serial and parallel example data
#plot_example_serial_and_parallel()
# run the test
#unittest.main(verbosity=2)The first half of this script demonstrates the function plot_example_serial(),
which sends some sample initial data to heat_serial(), computes a solution,
and then plots the result. This can be tested using the standard
$ python test_homework4.py
Once you have implemented heat_parallel(), you can test your code against the
test suite by uncommenting the last line, unittest.main(verbosity=2),
commenting the rest of the script, and running
$ mpiexec -n 3 python test_homework4.py
This will call heat_parallel(), passing in some sample initial data and
running the test defined above in test_heat_parallel(). You can plot your
results on top of the serial code output by uncommenting the function call
plot_example_serial_and_parallel().
Please answer the following questions in report/report.pdf. Most of these
questions will test your ability to read and understand the code in
test_homework4.py.
-
(10 pts) Following the syntax of the function
test_homework4.py:plot_example_serial_and_parallelcreate a single plot using the example initial condition displaying the results ofNt = 100, 200, 300, 400. Just as inplot_example_serial_and_parallel()plot the parallel solutions (as a solid red line) for each of these values ofNton top of the serial solutions (as a thick, dashed red line). Again, each of these solutions for the varyingNtshould be on the same plot. -
(10 pts) Modify the example in
test_homework4.py:plot_example_serial_and_parallel()to compute the solution to the heat equation with the original intial dataN = 96 # number x,u-points in entire domain Nx = N // comm.size # number x,u-points in each process's chunk dx = 1.0/(N+1) # step size in x-domainbut with
dt = 0.501*dx**2In the plot you should see that the solution curve is beginning to appear "jagged". Save this plot in your report. Save another plot in your report with
dt = 0.505*dx**2and one more withdt = 0.51*dx**2. This last "solution", especially, should appear highly oscillatory and is, in fact, very incorrect in that it is not a solution to the heat equation.These three plots are examples of "numerical instability". It is a central topic in numerical analysis and numerical solutions to differential equations.
-
(10 pts) How will you be using the tools we learned in this class within your own work? Please explain in at least three sentences. I am genuinely interested in what kinds of projects you will pursue after this class!
Provide documentation for the function prototypes listed in all of the files in
include/ following the formatting described in the
Grading document.
Because most of the code has been written for you, you will not be judged on performance in this homework assignment.