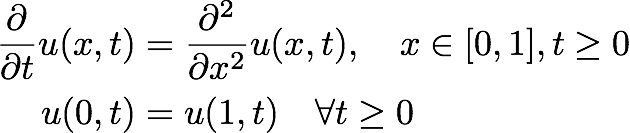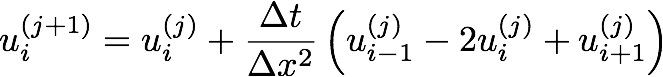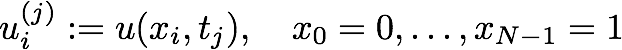Homework #4

In Homework #4 we will solve the heat equation using MPI via a domain decomposition method similar to the technique used in the array shift code from Lecture #15. This assignment will require that you read more code than you will write.

Important: this assignment requires that mpi4py be installed in your compute environment:

$ pip install mpi4py

Your homework tests will not work until this is installed!

Compiling and Testing

The makefile for this homework assignment has been provided for you. It will compile the source code located in src/ and create a shared object library lib/libhomework4.so.

Run,

$ make lib

to create lib/libhomework4.so. This library must exist in order for the Python wrappers to work. As a shortcut, running

$ make test

will perform the parallel tests:

$ make lib
$ mpiexec -n 3 python test_homework4.py

Important: Read the contents of test_homework4.py to get an idea as to what is going on when you run mpiexec -n 3 python test_homework4.py after implementing src/heat.c:heat_parallel(). The observant student will realize that each process is running it's own version of the test suite. However, only Process 0 will actually compare the parallel solution to the serial solution.

The test suite test_homework4.py also contains some code for generating plots of an example heat equation problem using both the serial and the parallel versions. Usage of these functions are demonstrated within the two provided plotting functions as well as in the if __name__ == main` block at the bottom of the test script.

Assignment

In this assignment we will numerically solve the periodic heat equation

using the Forward Euler method

where

First, read the contents of src/heat.c:heat_serial(). This is a completely serial implementation of Forward Euler for solving the heat equation. To see this in action, compile src/heat.c into a shared object library via make lib and then run the test suite:

$ python test_homework4.py

In particular, make sure that only the plot_example_serial() function is called when run. (As in the original state of the test script.) This will create a plot called serial_heat.png in your project directory.

Some key things to observe about heat_serial():

• This function solves the heat equation on input data u representing an initial condition on the whole interval x \in [0,1]. The input example data is defined in test_homework4.py.
• The outmost loop within the function performs the time iteration.
• The inside loop performs Forward Euler on the interior nodes of ut to obtain the interior nodes of utp1. That is, the loop only computes the iterates: utp1[1], ..., utp1[Nx-2].
• After the inside loop, we separately iterate at the "boundaries". (Quotation marks used because we're acutally solving the periodic problem so there really isn't a boundary.) That is, since we're solving the periodic problem the solution at utp1[0], for example, uses the data at ut[0], ut[1], and ut[Nx-1].

Next, read the contents of test_homework4.py. In this homework assignment the test suite that we will use against your implementation of src/heat.c:heat_parallel() has been provided to you. See the section "1) Tests - 60%" below for more information.

Implement These Functions:

Finally, write the requested C/MPI code. Implement the function described below. (Only one function in this homework.) As usual, homework4/wrappers.py contains the Python wrappers for the C functions you will be using.

• src/heat.c:heat_parallel()

  Much of the boilerplate has been written for you. You will be asked to write the "interesting part" using the appropriate MPI functions. Following the pattern of shift.c in Lecture #15, write heat_parallel() such that it behaves in the following way:

  • Each process such that each process recieves a "chunk", double* uk, of the solution vector. Note that, as in shift.c, each process will call heat_parallel() setting its own values for rank and size via MPI_Comm_rank() and MPI_Comm_size(), respectively. These chunks represent parts of the "whole" solution, u. That is, if the whole data array u is N elements long then Process 0 receives the first Nx elements of u, Process 1 receives the next Nx elements, etc., and Process size-1 receives the last Nx elements where Nx = N / size.

    Here's a picture similar to that in Lecture #15's shift.c to better explain the situation:

      Proc0     Proc1     Proc2
    [a, b, c] [d, e, f] [g, h, i]
        *--*---*
           ^
           |
         computing solution at this point
         in Proc 0 requires knowing the
         left-boundary data at Proc 1
    
    "Whole data array": u = [a, b, c, d, e, f, g, h, i]
    Proc 0: uk = [a, b, c]
    Proc 1: uk = [d, e, f]
    Proc 2: uk = [g, h, i]
    
    (Computing the solution at `b` using Forward Euler only requires `a`, `b`,
    and `c` so it can be done without needing to communicate data to other
    processes.)
    

  • Each process should numerically solve the heat equation within its own chunk, communicating the required boundary data to "adjacent" processes as necessary. Note that the data communication is necessary because computing uktp1[0] requires knowing the right-boundary value of the ut array belonging to the left process. In other words, computing uktp1[0] at process k requires the value of ukt[Nx-1] at process k-1. Similar data transfers need to occur at the right boundary, uktp1[Nx-1] of process k.

  • Because we wish to solve the periodic heat equation problem, the rank = 0 process needs to communicate its boundary data with the rank = size - 1 process and vice-versa. (In addition to the necessary boundary communication between processes at rank k-1, k, and k+1 for all k.)

The wrapper function homework4/wrapper.py:heat_parallel() calls src/heat.c:heat_parallel(), passing in an MPI_Comm object which is generated by mpi4py. See the test script for example usage of this wrapper function within a parallel context.

1) Tests - 60%

Because we haven't discussed mpi4py in much detail the test suite that we will use against your code has been provided to you. Please read the contents of test_homework4.py. Again, note that the parallel test code is to be executed via

$ make lib
$ mpiexec -n 3 python test_homework4.py

meaning that each spawned process will be running the test suite on its own. (However, only Process 0 concatenates the parallel results and compares with the serial solution.)

Make sure your implementation of src/heat.c:heat_parallel() causes the test to pass. You only have one test so make it count!

Some additional functions have been provided to you within test_homework4.py demonstrating how to, for example, call heat_parallel() and plot the results. In particular, take a look at the example usage provided to you at the bottom of the test script:

if __name__ == '__main__':
    # plot the serial result to see what kind of initial condition and solution
    # is expected.
    #
    #     $ python test_homework4.py
    #
    # (Comment this out when running parallel tests. See below.)
    plot_example_serial(chunks=3, Nt=100)

    ###################################################
    # RUN THE TESTS AND PARALLEL PLOT BELOW USING MPI #
    #                                                 #
    #     $ mpiexec -n 3 python test_homework4.py     #
    #                                                 #
    # (Comment out the serial plot, above, and remove #
    #  the comments below to run the tests!)          #
    ###################################################

    # plot the serial and parallel example data
    #plot_example_serial_and_parallel()

    # run the test
    #unittest.main(verbosity=2)

The first half of this script demonstrates the function plot_example_serial(), which sends some sample initial data to heat_serial(), computes a solution, and then plots the result. This can be tested using the standard

$ python test_homework4.py

Once you have implemented heat_parallel(), you can test your code against the test suite by uncommenting the last line, unittest.main(verbosity=2), commenting the rest of the script, and running

$ mpiexec -n 3 python test_homework4.py

This will call heat_parallel(), passing in some sample initial data and running the test defined above in test_heat_parallel(). You can plot your results on top of the serial code output by uncommenting the function call plot_example_serial_and_parallel().

2) Report - 30%

Please answer the following questions in report/report.pdf. Most of these questions will test your ability to read and understand the code in test_homework4.py.

• (10 pts) Following the syntax of the function test_homework4.py:plot_example_serial_and_parallel create a single plot using the example initial condition displaying the results of Nt = 100, 200, 300, 400. Just as in plot_example_serial_and_parallel() plot the parallel solutions (as a solid red line) for each of these values of Nt on top of the serial solutions (as a thick, dashed red line). Again, each of these solutions for the varying Nt should be on the same plot.

• (10 pts) Modify the example in test_homework4.py:plot_example_serial_and_parallel() to compute the solution to the heat equation with the original intial data

  N = 96               # number x,u-points in entire domain
  Nx = N // comm.size  # number x,u-points in each process's chunk
  dx = 1.0/(N+1)       # step size in x-domain
  

  but with

  dt = 0.501*dx**2
  

  In the plot you should see that the solution curve is beginning to appear "jagged". Save this plot in your report. Save another plot in your report with dt = 0.505*dx**2 and one more with dt = 0.51*dx**2. This last "solution", especially, should appear highly oscillatory and is, in fact, very incorrect in that it is not a solution to the heat equation.

  These three plots are examples of "numerical instability". It is a central topic in numerical analysis and numerical solutions to differential equations.

• (10 pts) How will you be using the tools we learned in this class within your own work? Please explain in at least three sentences. I am genuinely interested in what kinds of projects you will pursue after this class!

3) Documentation - 10%

Provide documentation for the function prototypes listed in all of the files in include/ following the formatting described in the Grading document.

4) Performance - 0%

Because most of the code has been written for you, you will not be judged on performance in this homework assignment.