The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as possible. For more information: knapsack problem
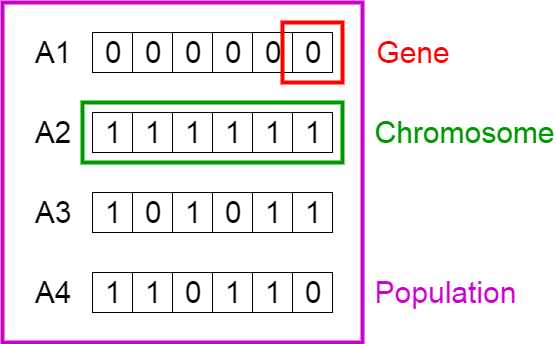
A genetic algorithm (GA) is a metaheuristic inspired by the process of natural selection that belongs to the larger class of evolutionary algorithms (EA). Genetic algorithms are commonly used to generate high-quality solutions to optimization and search problems by relying on bio-inspired operators such as mutation, crossover and selection. John Holland introduced Genetic Algorithm (GA) in 1960 based on the concept of Darwin’s theory of evolution; afterwards, his student Goldberg extended GA in 1989. For more information: genetic algorithm
- BEGIN
- Initialise
- Evaluate
- Repeat:
- Parent Select
- Recombine
- Mutate
- Evaluate
- Survivor Select
- END
I recommend using a virtualenv:
$ git clone https://github.com/zahidkizmaz/Knapsack-Problem_GA
$ cd Knapsack-Problem_GA/
$ python3 -m venv venv
$ source venv/bin/activate
(venv) $ pip install -r requirements.txt
(venv) $ cd source/
(venv) $ python main.py ../tests/test1.txt > out1.txt
After this you should be able to see a graph and a out1.txt contains informaton about the genetic algortihm results.
You can provide hyper parameters in a txt file as an argument to main.py. Input file must be txt file formatted like this:
- Random number list between [0,1] and seperated with comma
- Population Size
- Tournament Size for tournament selection (k)
- Mutation rate between [0,1]
- Total iteration number
- Bag size
- Weights of items seperated with comma
- Values of items seperated with comma
Here is an example txt file:
0.06,0.32,0.87,0.02,0.15,0.47,0.36,0.53,0.32,0.39,0.39,0.26,0.27,0.21,0.73,0.42,0.69,0.32,0.3
30
5
0.07
82
47
14,13,11,13,10,11,13,14,11,13,15,11,11,11,5,15,15,6,12,12,7,8,6
18,22,21,23,18,22,19,22,25,17,23,21,11,13,20,11,13,14,15,17,25,14,17
This graph indicates a summary of the population at the given iteration. Best is the highest fitness value in the population and worst is the lowest fitness value in the population. Also average indicates for average fitness value for all population at the corresponding iteration.