- 백준과 프로그래머즈 사이트에서 풀었던 문제들에 대한 코드를 올려놓은 repository입니다.
- 코드(이하 솔루션)는
src폴더에서 확인하실 수 있습니다.- 백준 문제에 대한 솔루션은 문제 닉네임과 문제 번호가 함께 표기되어 있습니다.
- 프로그래머즈 문제에 대한 솔루션은 문제 닉네임만 표기되어 있습니다. 이 repository 내에서 따로 분류해야 할 것 같습니다.
- 모든 솔루션에 대한 언어는 java 및 python 입니다.
- (2020/09/25) 못 풀었지만 생성된 문제에 대한 파일은
${filename}_(unsolved)표시를 하기로 하였습니다.
- 코드(이하 솔루션)는
- leetcode와 codeforce 문제들을 일부 추가하였습니다.
-
- 굳이 String을 만들 필요 없이 개수만 계산하면 되는 것임
-
- lower_bound 또는 upper_bound 구현
- python 으로 시도했는데 TO로 실패함.
bisectlibrary 이용해서 풀음.
-
한윤정이 이탈리아에 가서 아이스크림을 사먹는데 (백준)
- 핵심은 배열을 활용하는 것
- 금지 조합은 2가지인데, 선택 조합은 3가지
- 여기서는 선택 조합 보다는 금지 조합에 대한 배열을 만들고, 선택 조합을 금지 조합에 대입시켜보는 것이 맞다.
- 예) (1,2,3) -> (1,2), (2,3), (1,3) 확인
- python lib의
itertools.combinations는 시간이 너무 오래걸림 - 다중 for문으로 푸는것이 훨씬 빠름 (약 3배정도)
- 핵심은 배열을 활용하는 것
-
- bfs 로 해결하는 것인데, 테스트 케이스가 부족하여서 조금 쉬운 문제가 되버림 (하지만 난 못풀었음)
- 핵심은 memoization도 적절히 섞어줘서 가지치기를 진행하는 것
- python에서의 상하좌우 이동은 tuple로 해결하는 것이 좋다는 것을 깨달음
- python에서의 queue는 list 보다는 collections의 deque를 사용하는 것이 좋다는 것을 깨달음
-
- BFS보다 DFS를 사용하는게 빠른 문제
- 자는 쓰지 않음
- 각도의 개념을 이해하는게 중요했음
-
- 구현은 어렵지 않았는데, 경우의 수가 핵심이었다.
- 사탕끼리 바꾼 행,열 만 고려해야되는게 아니라, 이미 바꾼 상태에서도 얻을 수 있는 최대값이 다른 어디엔가 존재한다.
- 구현은 어렵지 않았는데, 경우의 수가 핵심이었다.
-
Maximum Sum Obtained of Any Permutation (leetcode)
- 주어진 여러개의 구간들 중 가장 많이 중첩된 순위를 한꺼번에 계산하는법
- 핵심 :
시작 구간에는1그리고마지막 구간 + 1에는-1을 놓고(더하고) 굴린다..!
- 핵심 :
- 주어진 여러개의 구간들 중 가장 많이 중첩된 순위를 한꺼번에 계산하는법
-
Split a String Into the Max Number of Unique Substrings
- 풀긴 풀었는데 재귀로 풀었다가 TLE 나버린 case
- Backtracking 솔루션을 보니 훨씬 깔끔했다. 다만 이해하긴 좀 어려웠음.
- 풀긴 풀었는데 재귀로 풀었다가 TLE 나버린 case
-
- 두가지 해결 방법이 있는 문제
- Sliding window Maximum 활용 (나는 이 방법을 썼다.. 이해하는데 오래걸렸다)
- 이진 탐색하면서 일일이 check
- 두가지 해결 방법이 있는 문제
-
- 문제는 잘 풀었는데, python의
deque와array의loop에 관련하여 할말이 있다.for i in range(len(deque))가while len(deque) >= 1보다 확실하게 현재deque에 포함된 모든 내용을 확인한다.while의 경우,while문 내에서deque값이 추가되면 그 값도 꺼내지게 된다.
- 2차원
array의loop의 경우, 특정 값t가 존재하는지 확인하고 싶다면 다음처럼 하면 좋다.
for i in array: if t in i: print('exist!')
- 문제는 잘 풀었는데, python의
-
- 핵심: 크기가
n인 배열 중 특정 원소의 개수가⌊n/2⌋보다 많은 원소는 반드시 한개만 존재한다.- 그럼
⌊n/3⌋의 경우는 ?
- 그럼
- 핵심: 크기가
-
- 움직이면서 자원을 충전 그리고 소모를 반복하는 문제
- 두 가지만 파악하면 되었다.
- 움직이는 사이에 문제가 없음을 확인 모든 자원 >= 소모 자원
- (1)이 확인되었다면, 반드시 정답은 존재
->0~n방향으로 자원 충전 및 소모 진행하면서 시작 위치 찾기
- 두 가지만 파악하면 되었다.
- 움직이면서 자원을 충전 그리고 소모를 반복하는 문제
-
- combination을 구하는 방식이 잘못되었다.
- 부분 수열에서 combination 구하는 것은 sliding 방식으로 구해야 한다.
(1,2,3) -> (1,2), (2,3), (1,2,3)
- 부분 수열에서 combination 구하는 것은 sliding 방식으로 구해야 한다.
- combination을 구하는 방식이 잘못되었다.
-
- dfs (또는 bfs) + memoization 사용 문제
- memoization 업데이트 방식이 내가 경험한 것과 다르다.
- 주워 들음) dp는 한번 정하면 일반적으로 절대 수정하면 안되는 것을 원칙으로 하자.
- 이 문제의 경우, memoization의 이유 말고도, 이미 방문한 곳은 절대 방문하지 않는다.. 왜? 판다의 특성 때문에
- 다시 한번 살펴보는게 좋을 것 같다.
- dfs (또는 bfs) + memoization 사용 문제
-
- DFS에서 굳이 2d 배열로 연결되있지 않은 vertices 까지 체크할 필요가 없다.
set()또는list()가 들어간 2d 배열을 만들어서 연결되있는 것만 집어넣어 주자.- 그리고, dfs에서 이미 방문한 것을 확인할 수 있는 방법은
set()말고 bit manipulation이 있다.- 우선 방문한 노드가
i라고 가정하면,z += (1 << i)로z에 저장 - 이후 어떤 노드
k가 이미 방문했는지 확인하고 싶다면,(1 << k) & z == 1로 확인한다.
- 우선 방문한 노드가
- DFS에서 굳이 2d 배열로 연결되있지 않은 vertices 까지 체크할 필요가 없다.
-
- 가중치(cost)가 다른 문제에서의 BFS 사용: 이 문제는 cost가 다르다. (순간 이동 cost: 0, 움직임 cost: 1)
- 너무 길어지는것을 막기 위해, 최대한 빠른걸 먼저 해결해야 하고, 이를 위해 그냥 queue 대신 priorityQueue를 사용한다.
- 또한 문제 input에 대한 여러 경우의 수를 생각해보는 것을 잊지말자.
- 가중치(cost)가 다른 문제에서의 BFS 사용: 이 문제는 cost가 다르다. (순간 이동 cost: 0, 움직임 cost: 1)
-
- 이분 그래프의 정의
- 각 정점에 대해서 BFS 또는 DFS 사용
- BFS 또는 DFS를 사용하면서 특정 정점에 인접한 정점들은 특정 정점과 반대의 색을 칠한다.
- 칠하는 도중, 만약 이미 칠해진 정점을 발견한 경우, 그 정점이 인접한 정점과 같은 색이라면 이분 그래프가 아니다.
-
- 서로 붙여보면서 정렬하는 것이 핵심. 답은 정말 간단한데 너무 창의적이라 생각을 못했다.
-
- 주어진 배열의 두 숫자를 더해서 목적하는 값을 찾는 문제
O(n^2)은 너무 쉽고,O(n)으로 풀려면 hashtable을 사용해야 했다.- hashtable에 숫자를 넣으면서 동시에 체크하는 방법이 빠름
- 주어진 배열의 두 숫자를 더해서 목적하는 값을 찾는 문제
-
Maximum Number of Achievable Transfer Requests
- 최대/최소를 구하는 문제의 contraints가 작은 경우 (
1<= n<= 20,1<= request.length <=16), 모든 조합을 고려해볼 것itertools.combinations사용
- 최대/최소를 구하는 문제의 contraints가 작은 경우 (
-
- Local minima & local maxima를 구하는 문제
- 배열
a의 local minima란,i번째 원소a_i가a_(i-1) >= a_i && a_i <= a_(i+1)를 만족하는 경우 (구덩이, valley) - local maxima는 그 반대, 즉,
a_(i-1) <= a_i && a_i >= a_(i+1)(동산, peak)
- 배열
- 배열에서 최대의 합을 구하는 문제가 있다면, 그 값들을 시각화 하는 것도 문제를 파악하는데 도움이 된다.
- 만약 + 로 시작해서 -, +, -, + 이런 순으로 원소들의 최대 합을 구하는 문제가 있다면, 반드시 정답은 홀수 번 합이다 (e.g. + - +).
- Local minima & local maxima를 구하는 문제
-
- Sliding Window를 활용 해서 해결하는 문제
[1, 2, 3]이 가질 수 있는 총 subarray가 a개인 경우,
[1, 2, 3, 4]의 총 subarray는a + end - start = a + 4 - 0가 된다.- 여기서
start는1의 index, 그리고end는4의 index + 1
- 여기서
- 이러한 특징을 활용하여 array에서 window를 놓고 sliding 시키면서 product 값 그리고 subarray 개수를 계산하면 됨
- Sliding Window를 활용 해서 해결하는 문제
-
- 문제 자체는 쉬웠는데, 짝수
n명을 반/반 두 팀으로 나누는 조합에 대하여 할말이 있다.python의itertools.combinations()에서 생성된 조합을 절반으로 나누면 위 조합이 만들어진다.- 예를 들어
n=4명의 조합은(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)인데, 이를 절반으로 나누면 정확히 반/반 조합이다. - 즉,
A = (0, 1), (0, 2), (0, 3)/B = (1, 2), (1, 3), (2, 3)으로 나누고,A[i]는B[n-i-1]와 정확히 매칭된다.
- 예를 들어
- 문제 자체는 쉬웠는데, 짝수
-
- 조그만 2차원 배열을 쉽게 다루는 방법
3x3배열인 경우(0,0)부터(2,2)까지 각 원소들을 하나의 문자열로 표현한다. (e.g.123456780)
- 조그만 2차원 배열을 쉽게 다루는 방법
-
- 문제는 쉽지만, 더욱 효율적으로 풀 수 있는 방법이 존재한다.
- 길이가
n인 배열a에 포함되지 않은 가장 작은 양수는 반드시1~(n+1)사이의 값이다. - 그리고,
a의 원소의 크기가1이상n미만이라고 할 때, 해당 원소의 등장 횟수를a자체에서 셀 수 있다.a의 원소를 인덱스로 여기고 길이를 더해준다 ->a[a[i]%n] += n- 이후
a[i] // n == 0인 경우, 그i값은a에 원래 존재하지 않았던 원소라는 것을 체크할 수 있다 (출처).
- 길이가
- 문제는 쉽지만, 더욱 효율적으로 풀 수 있는 방법이 존재한다.
-
- Counter를 활용하는 문제: 리스트가 주어졌을 때,
b-a == k, a <= b를 만족하는 쌍(a, b)찾기- 리스트의 모든 값들을 Counter에 넣은 다음,
Counter[b-k]가 하나라도 count 되었다면, 그 쌍(a, b)는 리스트에 존재함
- 리스트의 모든 값들을 Counter에 넣은 다음,
- Counter를 활용하는 문제: 리스트가 주어졌을 때,
-
- Rotate 하는 list를 만들기
- 우선 list를 circular 하게 만들자 (꼬리가 머리를 가리키는 식으로).
- 그리고, 그 꼬리에서 다시
len(list) - (k % len(list))만큼 이동한 후(k는 list 이동 횟수), 도착한 list의 노드가 꼬리가 된다.- 그 노드(
A)를 꼬리로 만드는 방법:head = A->next그리고,A->next = None
- 그 노드(
- Rotate 하는 list를 만들기
-
Count Subtrees With Max Distance Between Cities
- Tree에서 가능한 모든 Subtree를 찾는 방법: 가능한 모든 vertices의 조합을 찾아내서, 그것이 tree 인지 확인
- 가능한 모든 vertices 조합을 찾는 방법:
combinations또는bitmasking사용 - Tree인지 확인하는 방법:
BFS또는DFS로 조합에 존재하는 정점 간 거리를 구하고, 만약 구할 수 없다면 tree가 아님BFS방법(다익스트라 응용): 초기 거리를 무한으로 설정(시작 노드만 0),queue를 이용해서 정점을 넣고 빼고, 이웃 정점 거리 = 이전 정점 거리 + 1
- 가능한 모든 vertices 조합을 찾는 방법:
BFS로 풀어보는 것을 권장
- Tree에서 가능한 모든 Subtree를 찾는 방법: 가능한 모든 vertices의 조합을 찾아내서, 그것이 tree 인지 확인
-
- 예외 케이스를 기억하자: 1) 불은 한개가 아닐 수 있다, 2) 미로의 크기가 최소인 경우 (1 by 1)
-
AAABB로 팬린드롬 만들 때 ->ABABA가BAAAB보다 사전 순 먼저임- 위의 경우, 홀수나 짝수 상관없이 알파벳 순으로 절반씩 붙여주고, 가운데 하나만 홀수 알파벳을 붙인다 (
AB+A+BA)
- 위의 경우, 홀수나 짝수 상관없이 알파벳 순으로 절반씩 붙여주고, 가운데 하나만 홀수 알파벳을 붙인다 (
-
- Merge Sort를 활용하여 linked list 정렬하기
- Top Down 방식과 Bottom Up 방식이 존재함
- Top Down: O(nlog(n))의 Time complexity 그리고 O(log(n))의 Space complexity
- O(log(n))은 recursive call stack의 추가 공간 요구 때문에 발생 (트리의 높이라고 생각하면 됨)
- Linked list의 중간 node 찾는 법: head에서부터 하나는 1 node, 다른 하나는 2 node 씩 움직이는 pointer를 활용
- Merge 방법: dummy head를 만들고, 합치려는 두 list의 node 중, 작은 값부터 순서대로 dummy에 엮어줌
- Bottom Up: O(nlog(n))의 Time complexity 그리고 O(1)의 Space complexity
- 아직 자세히 확인하지 못함
- Top Down: O(nlog(n))의 Time complexity 그리고 O(log(n))의 Space complexity
- Top Down 방식과 Bottom Up 방식이 존재함
- Merge Sort를 활용하여 linked list 정렬하기
-
- Given an array, rotate the array to the right by
kstep - O(n)의 Time complexity 그리고 O(1)의 Space complexity로 rorate하기
- 예시로 이해하는 것이 빠르다. 배열 A:
[1,2,3,4,5]->[4,5,1,2,3](Whenk=2) - 일단 A를 뒤집어보면:
[5,4,3,2,1].. 패턴이 보이는가?[/5,4/3,2,1/]:/로 나눠진 부분을 뒤집어 주면된다.
- 예시로 이해하는 것이 빠르다. 배열 A:
- Given an array, rotate the array to the right by
-
132 Pattern (Keyword: Stack)
n개의 원소를 가진nums배열이i < j < kandnums[i] < nums[k] < nums[j]를 만족하는지 확인하는 문제- 핵심은
i < j면서nums[i] < nums[j]를 만족하는j를 먼저 찾고, 그 다음j를 중심으로 조건을 만족하는k를 찾는다.j를0~len(nums)-1까지 움직이면서i_nums[j]을 updatei_nums[j]이란,nums의j번째까지의 원소 중 가장 작은 원소를 의미: 이것이i가 됨
- 만약,
i_nums[j] < nums[j]라면, 반드시i < j와nums[i] < nums[j]를 만족하는j가 있다는 뜻임 - 그리고
j + 1이후부터 조건을 만족하는k를 찾으면 된다.
- 위 방법은
O(n^2)방법이다. 하지만, binary search를 이용하는O(nlog(n))그리고 stack을 이용하는O(n)방법이 존재함 - 더 좋은 방법은 이후에...
-
- 일련의 양의 정수 높이가 존재하는
n개의 블럭들이 주어지고, 블럭에 물을 부었을 때 얼마나 많은 물이 블럭에 잠기는지 세는 문제 - 핵심:
i번째 블럭이 보유할 수 있는 물의 높이H를 다음과 같이 구할 수 있다.0~i번째 블럭 중 가장 높은 높이A,i~n-1번째 블럭 중 가장 높은 높이BH = min(A,B) - h(h는i번째 블럭의 높이)- 물론,
min(A,B) > h의 경우만 위 식이 성립, 아니면H = 0임
- 물론,
- 시간 복잡도를 줄이기 위해 배열
left와right를 사용 (left[i]는A그리고right[i]는B를 저장하는 배열)
- Maximize Distance to Closest Person
- 풀이 방법이 비슷한 문제 (
left,right배열 활용) - 배열들을 사용하지 않고 공간 복잡도를 줄이는 방법: 어떤 좌석
i에서 가장 가까운 사람과의 거리는min(i - prev, future - i)임prev는i에서부터 가장 가까운 왼쪽 사람이 앉은 자리,future는i에서부터 가장 가까운 오른쪽 사람이 앉은 자리future를 위해 python에서generator를 활용할 수 있음
- 풀이 방법이 비슷한 문제 (
- 일련의 양의 정수 높이가 존재하는
-
- min heap & max heap 두 개를 동시에 사용하는 문제
- 전체 배열
A중에서 min heap은 내림차순 담당, max heap은 오름차순 담당 A = [1,2,3,4,5]의 경우 min heap:[5,4], max heap:[1,2,3]
- 전체 배열
- 정렬된 배열의 중간값(median)을 출력해야 하므로, 두개의 heap 길이를 비슷하게 유지한다.
- max heap에 우선적으로 값을 넣고, 1개 이상 길이가 차이날 경우 min heap에 넣는다.
- max heap의 root 값이 배열의 median 값이라고 정하자.
- 이 경우, 매번 두 heap 중 하나에 값을 넣을때마다, max heap의 root 값이 min heap의 root 값보다 크면 교환한다.
- Why?
- 각 heap의 오름차순과 내림차순을 유지해야하므로
- 배열의 길이가 짝수일 경우, median은 중간에 있는 두 수 중에서 작은 수이므로
- min heap & max heap 두 개를 동시에 사용하는 문제
-
- 샴페인을 부워서 특정 잔에 얼마나 많은 물이 남아있는지 알아내는 문제
- 잔에 물을 한컵씩 붓는다고 생각하지 말고, 한번에 다 따라버렸을 때 어떻게 흘러가는지 파악하는게 핵심이다.
-
- 트리의 지름이란, 트리에서 임의의 두 점 사이의 거리 중 가장 긴 것을 말한다.
- 구하는 방법: 임의의 노드
A에서 가장 거리가 먼 노드B를 찾는다. 다시,B에서 거리가 가장 먼 노드C를 찾으면,B와C의 거리가 트리의 지름이 된다. - Minimum Height Trees
- tree-like graph에서 가장 짧은 높이를 가진 tree의 root node를 찾는 문제
- 트리의 지름에 가장 가운데 존재하는 노드(들)을 찾으면 된다.
- 이러한 노드들을 centroids 라는 별명으로 부르는데, tree-like graph에서 centroids는 반드시 2개 이하임이 증명되어있다.
- 푸는 방법은 두 가지: 1) 트리의 지름을 구하면서 지름을 이루는 노드 경로 찾기 2) Topology sort
- Topology sort의 경우, BFS로 해결한다.
즉, graph의 leaf node들을 모두 큐에 넣고, 안으로 조금씩 들어가면서 최종적으로 두 노드만 남을 때까지 방문한 노드들을 graph에서 제외시킨다. 그리고 남은 두 노드가 centroids가 된다.
-
- 'abcd'와 'ab*d'가 일치하는지 확인하는 법
- '*' 을 제외한 나머지 문자('ab' 그리고 'd')가 동일할 경우
- '' 을 제외한 나머지 문자 길이 + ''에 해당하는 길이가 같다면, 두 문자열이 동일하다고 판단한다.
- 'abcd'와 'ab*d'가 일치하는지 확인하는 법
-
Check Array Formation Through Concatenation
list간+로 합칠 수 있다[1,2] + [3,4] = [1,2,3,4]
dict의get함수가 유용하다-
mp= {1: [5]} a = mp.get(1, []) # a = [5] b = mp.get(2, []) # b = []
-
-
Convert Binary Number in a Linked List to Integer
- linked list에 포함된 값을 정수로 바꾸는 문제
<<와|를 활용하면 공간 복잡도O(1)로 해결할 수 있다.
-
- 적은 수에 대한 조합을 고를 땐, 객기 부리지 말고
O(n^2)으로 단순히 생각하자.
- 적은 수에 대한 조합을 고를 땐, 객기 부리지 말고
-
- 대괄호 내 알파벳을 배수로 만드는 문제 (e.x.
"3[a]2[bc]"->aaabcbc) - DFS랑 stack을 사용하는 방법이 존재하는데, stack을 사용하는 방법 도 괜찮은 것 같다.
- 대괄호 내 알파벳을 배수로 만드는 문제 (e.x.
-
- 문자열 중 문자 하나만 빼서 palindrome이 되는 것이 가능한지 확인하는 문제
- two pointer를 문자열 양 끝에서 설정하고, 양쪽에서 가운데로 이동하면서 서로 일치하는지 확인한다.
- 만약, 서로 일치하지 않는 두 문자 A, B가 발생하면, 그때까지 일치한 문자열을 제외하고, A 또는 B를 제외했을 때 palindrome이 발생하는지 확인한다.
aaacdcc의 경우d를 빼는 것이 맞다.(aa)[a]{c}[d](cc)왼쪽 처럼,()소괄호에 있는 문자열은 무시하고,[]대괄호에 있는 문자 중 하나를 제외 후{}와 합쳐서 palindrome이 발생하는지 확인한다.
-
- binary Tree로 이루어진 집 구조; 부모 노드의 값을 가지면, 자식 노드의 값을 못가지는 규칙에서, 최대 가질 수 있는 값 찾기
- DFS에서 시간초과 발생 시, memoization으로 해결할 수 있는지 확인
- Hashmap(
dict)에서 class instance도 hashing이 가능하다(=key로 활용할 수 있음). - Memoization을 굳이 하나의 자료구조로 수행할 필요는 없음. 두 개 이상으로 사용해도 됨.
- Hashmap(
- DFS로 안될 것 같으면, DP 도 고려할 수 있음.
- 솔루션이 꽤 잘되어 있음
-
- stack을 활용한다(우선순위 연산자('*','/')가 나오면 stack에서 pop, 아니면('+','-') push)).
- 항상 '+' 가 있다고 생각하고 계산한다. (e.g.
1+2+3->+1+2+3), 시작 연산자가 '+'.
-
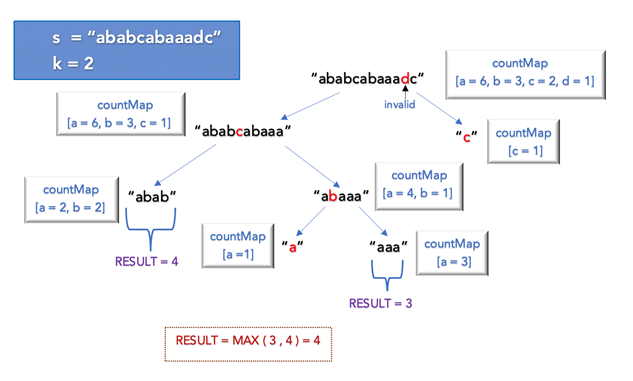
Longest Substring with At Least K Repeating Characters
- Divide Conquer 또는 Sliding Window를 사용하여 해결하는 문제
- Divide Conquer
- Sliding Window: 분할 정복보다 좀 더 복잡한 솔루션 (아직 이걸로 풀어보지 못함)
- Window를 움직이는 기준은 문자열
s의 unique 문자 개수0 < curr_unqiue < len(set(s)) - 현재 Window에 포함된 unique 문자열 개수가
curr_unqiue보다 낮을 경우 Window를 오른쪽으로 확장, 그 반대의 경우 왼쪽으로 축소 - 윈도우를 옮기면서, 윈도우에 포함된 문자열의 모든 알파벳이
k이상 존재하면, 그 길이들 중 최대값이 정답
- Window를 움직이는 기준은 문자열
-
- 배열에 존재하는 양 원소들이 서로
1이 아닐 경우 count 하는 문제 - 예시)
a = [1,0,0,0,1]의 경우a[2]만 count 된다. - 체크 방법
if a[i] == 0 and (i == 0 or a[i - 1] == 0) and (i == len(a) - 1 or a[i + 1] == 0):
- 배열에 존재하는 양 원소들이 서로
-
- greedy를 이용한 해법은 간단했지만, 그걸 떠올리기에는 역부족이였음
- 그리고 greedy인것을 알아도 시간초과를 피하기 위해선 조금 트릭이 필요했다.
- greedy는 경우의 수를 제한하는 방법이라는 것을 생각하자.
- 동전 뒤집기
- 이 문제도 비슷한 문제인데, 1차원 greedy가 2차원으로 확장되었다고 생각하면 됨.
- Combination 구할 때, bit masking을 사용하면 유용하다.
- 예시)
for i in range(0, 1 << n):-> 이렇게 하면2^n개의 조합(yes/no)을 구할 수 있다.
- 예시)
- 잡설) 이 문제를 python으로 푼 사람이 아무도 없음 (속도가 느려서), 나도 pypy3으로 채점했다.
- greedy를 이용한 해법은 간단했지만, 그걸 떠올리기에는 역부족이였음
-
- 30에 대한 배경 지식과 greedy를 이용하여 푸는 문제
- 깨달은점
- 어떤 수의 모든 자리의 수를 더해서 3으로 나눠지면 그 수는 3의 배수다.
- 배수 관련 문제가 나올때는 그 배수의 값들을 나열한 뒤, 패턴을 찾아보자.
- 입력값이 말도안되게 크면, 의외로 로직은 간단하다.
-
- 가장 큰 값을 받고, 가장 작은 값을 소모하면서 진행해 나가면 된다.
-
- priority queue와 greedy 문제
- 가장 크기가 작은 가방을 기준으로, 그 가방에 넣을 수 있는 보석들을 나열(
queue에 삽입)하고, 가장 큰 가치를 가진 보석을 뽑는다(pop).- 이런 방식으로 진행하면, 다른 가방도 체크할 때 한번 확인한 보석은 더 이상 크기를 비교할 필요가 없다.
- 가장 크기가 작은 가방을 기준으로, 그 가방에 넣을 수 있는 보석들을 나열(
multiset과 lower-bound를 활용해도 풀린다고 하는데, python은multiset대신sortedcontainers.SortedList()를 사용- 비슷한 문제로 순회강연, 과제 가 존재한다.
- 특정 날짜에 강연을 진행하면 하루가 지나므로, 그 날짜 이후의 강연들의 진행 유무에 영향을 받는다.
- 하지만, 그 날짜 이전의 강연들은 이미 지나갔으므로 진행 유무에 영향을 받지 않는다.
- 이러한 특징을 활용하여, 가장 강연 기한이 긴 날부터 짧은 날 순으로 내려가며,
해당 날짜부터 가능한 강연들만 선별하고(
n일 기준이면n, n+1, n+2, ...) 그 강연들 중 얻을 수 있는 최대 이득(강연료)을 찾는다(priority queue 이용).
- 이러한 특징을 활용하여, 가장 강연 기한이 긴 날부터 짧은 날 순으로 내려가며,
해당 날짜부터 가능한 강연들만 선별하고(
- priority queue와 greedy 문제
-
- 문제를 푸는 것보다 문제 자체를 이해하는데 어려워서 틀린 문제
- 1차원 좌표계에 존재하는
N개의 값들을K개의 연속된 그룹으로 나눴을 때, 각 그룹이 가진 범위들의 합의 최소를 구하면된다.- 예를 들어)
N = 5: 1 2 6 7 8그리고K = 2라면,[1 2] [6 7 8]로 나누는 것이 최소(1([1 2])+2([6 7 8])=3)다.
- 예를 들어)
-
Split Two Strings to Make Palindrome
- A의 prefix 와 B의 suffix를 붙여서 만든 palindrome C는 다음을 만족한다.
- A의 prefix 길이: N > B의 suffix 길이라면, A 앞에서 N 만큼 문자열은 B 뒤에서 N 만큼 문자열을 뒤집은 것과 같다.
- 그리고, C는 앞, 뒤 N 개의 문자를 제외한 가운데 문자열이 palindrome을 다시 이루고 있다.
- 예시) A:
ak/bbcc+ B:cc/bbka= Cakbbka(/는 prefix, suffix 구분 표시)- N: 2 => A 앞
ak, B 뒤ka그리고 가운데 문자열bb는 palindrome
- N: 2 => A 앞
- 다시 구현을 권장
- A의 prefix 와 B의 suffix를 붙여서 만든 palindrome C는 다음을 만족한다.
-
- 중복을 제거하면서 가장 사전 상 빠른 문자열을 만드는 문제 (
"cbacdcbc"->"acdb") - 문자열의 문자를 모두 count하고, 차례대로 문자를 stack에 넣으면서, stack의 밑바닥이 사전 상 가장 빠른 문자가 오도록 만든다.
- 단, 문자열에 등장한 문자는 적어도 한번씩은 등장해야 하므로, 문자 등장 횟수에 유의하면서 stack의 문자들을 조절한다.
- 예를 들어, stack에
bc가 있고a를 넣는다면, stack은a가 되야 하지만, stack의 값들이 각각 문자열의 하나밖에 없는 문자인 경우 빼지 않고 stack을bca로 만든다.
- 중복을 제거하면서 가장 사전 상 빠른 문자열을 만드는 문제 (
-
- heap을 어떻게 사용하는가?
- 가장 짧은 시간이 걸리는 것 중에서 가장 빠르게 요청이 온것을 처리함
- 그렇다고 또 디스크가 놀고있으면 안되므로, 아무리 짧은 시간이 걸려도 하는게 없으면, 도착한 요청을 바로 처리
-
- 정확성은 옳았으나, 효율적이지 못했음
-
- 핵심은 그리디 및 정렬
- 열에 따른 정렬 방법 (tie 해결)
array.sort(key=lambda x: (x[1], x[0]))- 두번째 열을 기준으로 오름차순 정렬 후, 두번째 열의 값이 서로 같으면 첫번째 열의 값으로 오름차순 정렬함
-
- min-heap을 활용하는 문제
- 모든 강의실의 시간을 빈틈없이 채우기 위해서, 가장 빨리 끝나는 강의실(min-heap)부터 차례로 강의 시간을 채워넣는다.
- 만약, 주어진 강의 시간 구간이 어느 강의실에도 매칭되지 않다고 판단(heap root 비교)되면, 새로운 강의실을 생성한다(heap item 삽입).
- min-heap을 활용하는 문제
-
2016-09-15 01:00:04.002와 같은 시간 문제를 다룰 때 팁time모듈은 소수점sec를 지원하지 않는다. 정수 시간만 지원 (e.g.01:00:04)- 년, 월, 일이 문제에 의미가 없다면, 시간을 초 단위로 변경하는 것이 편하다.
- 년, 월, 일의 초 단위 변환이 필요하면 python tip 참조
- 어떤 시간
t로 부터 1초 범위는 1000ms 단위로 생각했을 때,t ~ t + 0.999sec까지다 (t ~ t + 1 sec아님!). - 소수점 덧셈, 뺄셈은 이상한 계산 결과를 종종 내놓는다(e.g.
1 + 0.001 = 1.0010000004).- 이런 경우 가장 확실한 방법은
Decimal모듈을 사용하는 것이지만,round를 이용해도 충분하다.
- 이런 경우 가장 확실한 방법은
-
- dp 문제인데, 타일 문제랑 비슷해서 햇갈렸다. 중요한점은 같은 값끼리 중복이 허용되지 않는 다는 점
- 타일은 이미 섞어놓은 조합에서 하나를 더 얹는 것인데, 거스름돈 문제는 개별적으로 올려놓는 느낌 ?
- 예를 들면, 5를 위해 2 + 1 + 1 과 1 + 1 + 2 은 타일에서 다르지만, 거스름돈에서는 같다. 즉, 1을 먼저 이용 후, 2를 처리해야함
- dp 문제인데, 타일 문제랑 비슷해서 햇갈렸다. 중요한점은 같은 값끼리 중복이 허용되지 않는 다는 점
-
Maximum Non Negative Product in a Matrix
- 두개의 dp 배열을 활용해야 하는 문제 (창의적이다)
- Maximum dp, Minimum dp !
- 두개의 dp 배열을 활용해야 하는 문제 (창의적이다)
-
- Maximum Non Negative Product in a Matrix 문제와 마찬가지로, 2개의 dp 배열을 활용해야 하는 문제다.
- 여기서는 특정 dp cell의 값을 정할 때, 어느 방향에서 오는가에 따라 dp 배열을 생성했다.
- Maximum Non Negative Product in a Matrix 문제와 마찬가지로, 2개의 dp 배열을 활용해야 하는 문제다.
-
- 여기서 dp는 Boolean 형
dp[i]로 표기될 수 있는데,dp[i]는 주어진 strings의i번째 substring까지, 주어진 dictionary로 만들 수 있는가 이다.- 예를 들어,
s = abcde , dict = ["abc", "de"]가 존재한다면,
dp[0] = True (empty string),dp[0] -> dp[3] = True (due to "abc"),dp[3] -> dp[5] = True (due to "de")가 된다.
- 예를 들어,
- 여기서 dp는 Boolean 형
-
- 배열이 원형인 경우에 DP를 적용하는 문제
- 두가지 case로 나눠서 각 case 마다 DP를 진행한 후, 둘 DP 계산 결과에서 가장 큰 값이 최종 정답이 된다.
0 ~ N-1개의 배열의 원소의 경우,0번째 집을 털거나N-1번째 집을 터는 경우로 나눠진다.- 이렇게 case를 나누면 배열이 원형이 아니라 그냥 직선 형태가 되는것을 확인할 수 있다.
- 배열이 원형인 경우에 DP를 적용하는 문제
-
- 문제를 가장 큰 증가 부분 수열로 착각했다. 문제를 똑바로 읽는 연습을 하자.
- 이 문제를
O(nlog(n))으로 푸는 방법은 이분 탐색을 이용하는 것, 그리고 수열을 찾아갈 때, 수열의 꼬리(오른쪽 끝)를 최대한 작게 만들어줘야 한다. - 인덱스 트리(Index Tree)를 이용해서도 풀 수 있다고 한다.
-
- 수열 + 연속 합 = Two Pointer 문제
- head와 tail pointer를 조금씩 움직이면서, 그 사이의 수열을 이용한다. (sliding window와 비슷하기도 함)
-
- Sliding window를 활용하는 문제
- 연속된 subarray 문제가 나오면 sliding window 개념을 활용하자.
- Sliding window를 활용하는 문제
-
- 주어진 binary number
a의 1의 보수b를O(log(n))으로 구하는 방법: 2^N-1-a=b(e.g.a= '1010,b= '0101')
- 주어진 binary number
-
- 원형 관련 문제에서는 queue를 생각하면 편하다.
- 시작
index를 0부터 시작해서, 모임 배열arr의k번째 사람을 계속 제외하는 경우는 아래와 같다.index = (index + k - 1) % len(arr)을 만족하는arr[index]를 지속적으로 지워주면 된다(pop).
-
- 주어진 4개의 2차원 점이 정사각형을 이루는지 확인하는 문제
- 정사각형은 반드시 두 종류의 길이를 가지므로(1.가로=세로, 2.대각선), 모든 꼭지점의 조합에 대한 길이를 구하고 집합에 넣어서 크기를 확인
-
- 정사각형 구석에서 레이저를 쏘면 튕겨서 어느쪽 구석에 도달할 것인지 맞추는 문제
- 튕기는 것을 고려하는 대신, 레이저가 일직선으로 나아간다고 가정하고 풀면 쉽게 풀린다.
p와q의 비율이 각각 홀수 또는 짝수냐에 따라서 도달할 구석이 달라지므로, 비율을 구하기 위해gcd(p,q)를 활용한다.
-
- 직사각형을 1 by 1 grid로 나누고, 사각형의 대각선 꼭지점을 이을 때, 대각선이 지나가는 사각형의 총 개수를 세는 문제
- 가로
W, 세로H일 때, 총 개수는W + H - gcd(W, H)gcd(W, H) == 1의 경우: 대각선으로 생각하지 말고, 대각선을 굽혀서 직사각형의 가장자리만 걸어서 간다고 생각해보자. 그러면 총W+H- 1 개를 지나게 된다.gcd(W, H) == n (n != 1)의 경우:gcd(W, H) == 1의 경우를 여러 번 나눈 직사각형이므로, 총 개수는n* (W/n+H/n- 1) 이다.
- 반으로 잘라서 왼쪽 오른쪽 탐색하는 방법 (general way)
mid = (start + end) // 2, 그리고search(start, mid)(왼쪽),search(mid + 1, end)(오른쪽)mid를 활용하고,start > end인 경우 중단
-
- 심사 시간을 이용해서 시간을 찾는 것이 아니라, 일단 시간을 추정하고 그것이 옳은지 확인
- 시간을 추정하는 방법은 이분 탐색을 이용
int(추정 시간값 / 각 심사관별 심사시간) = 심사관당 맡을 수 있는 입국자 수- 각 심사가 걸리는 시간은 심사관마다 독립적으로 동작함
- 심사 시간을 이용해서 시간을 찾는 것이 아니라, 일단 시간을 추정하고 그것이 옳은지 확인
-
- Dense Ranking 이라는 랭킹 산정 방식이 있다. 동일한 점수를 받은 사람에게는 동일한 등수를 부여하는 방식이다. (공동 1등 이런 식)
- 특정 사람에 대한 Dense Ranking을 쉽게 계산하기 위해서는 distinct한 score array를 만들면 된다.
- 또한 이분 탐색을 위한
bisect는 내림차순 배열에서 동작하지 않는다. 오직 오름차순만 된다.- 즉, 내림차순에서 동작하는 bisect를 직접 만들어야 한다.
- Dense Ranking 이라는 랭킹 산정 방식이 있다. 동일한 점수를 받은 사람에게는 동일한 등수를 부여하는 방식이다. (공동 1등 이런 식)
-
DFS의 Graph coloring을 이용하여 Cycle 을 찾는 방법
- 세 개의 집합(A, B, C): A는 초기 집합(처음에 모든 노드가 여기 있음)/ B는 후보 집합(cycle이 발생 가능한 노드)/ C는 확정 집합(cycle이 없는게 확인된 노드)
- 세 개의 집합를 만들고, DFS로 노드 방문 시, 세 가지 케이스를 다룬다.
- 그 노드가 A에 있을 경우: 그 노드를 A에서 B로 옮겨준다.
- 그 노드가 B에 있을 경우: B에 있는 노드들에 의해 cycle이 확실하게 발생했다.
- 그 노드가 C에 있을 경우: 이미 해당 노드는 cycle이 없는 노드다. 무시하면 됨.
- 모든 이웃 노드를 방문한 노드들은 cycle이 없는게 확실하므로, B에서 C로 옮겨준다.
- 모든 노드가 A에서 C로 옮겨졌으면 그 directed graph는 cycle이 없다.
- HashMap(
dict)을 이용하여 노드 간 이동을 기록하면, cycle에 해당하는 노드들을 알 수 있다. - 관련 문제의 특징: 트리를 어떤 순서대로 방문하려는데, 주어진 노드 순서로 방문이 불가능/가능 한지의 여부를 물어봄
- 관련 문제
-
- LCA 문제는 segment tree 또는 dp 를 이용하는 두 가지 방법으로 나눠진다.
- Segment Tree *
- DP *
-
Segment (or Segmentation) Tree & Index Tree
-
Fenwick Tree (Binary Indexed Tree)
- Segment Tree 보다 메모리를 절약할 수 있는 트리
-
- Segmentation Tree를 처음 구현해봄 (트리 생성, 수정, 구간 합)
-
- 구간의 합 대신, 최대값과 최소값을 segmentation tree로 구현
- 재귀에서
return을 이해하고 활용하는 연습이 더 필요함
-
- 트리 수정에서, 구간 곱의 경우, 구간 내 원소가 0 으로 수정될 경우 전부 꼬이게된다. 이런 경우, 수정할 원소가 속하는 구간만 트리에서 새로 계산한다.
-
-
Trie
-
HashMap(
dictin python)을 활용해서 만든 트리- 여러 단어들을 하나의 트리에 넣어서, prefix/whole word 처리를 할 때 유용하다.
- Trie 구조 생성 복잡도
O(L*N)(L: 문자열 최대 길이,N: 문자열 총 개수)
-
관련 문제들 (어려운 문제가 아닌 경우, Trie 를 따로 만들지 않고
set또는dict으로 풀린다))- 전화번호 목록, 개미굴
- 가사 검색
- 패턴 매칭 시, Trie 활용 팁 두가지
- 각 Trie node에
length변수 추가 후 Trie 구축중에 계산 (length: 해당 노드 이후 매칭되는 단어의 총 개수) - prefix 단어(e.g.
???ord) matching 에는 단어를 거꾸로 해서 넣은 Trie 사용, postfix 단어(e.g.ord???) matching 에는 일반 Trie 사용 - 만약 매칭해야되는 단어의 길이가 다양할 경우, 길이에 따른 여러개의 Trie를 구성하는 것이 좋다.
- 각 Trie node에
- 패턴 매칭 시, Trie 활용 팁 두가지
- 휴대폰 자판
- Trie에 포함된 전체 단어들에 대해서 한꺼번에 재귀로 계산할 수 있는가? (풀긴 풀었는데 코드를 다시 한번 생각)
-
관련 알고리즘
- KMP 알고리즘 (Knuth-Morris-Pratt string matching algorithm)
- 아호 코라식 알고리즘 (Aho-Corasick multiple pattern matching algorithm)
-
-
Union-Find
- 공항
g_i가 입력으로 들어온 비행기가 들어갈 게이트는1 <= g_i <= G인데,
최대한 많은 도킹을 위해선 오른쪽g_i부터 왼쪽1까지 찾아가면서 빈자리에 넣는 것이 맞다.g_i에 비행기를 넣으면 그 다음 도킹할 게이트는g_i-1이므로,g_i의 부모를g_i-1로 설정한다(union).- 위 과정에서
g_i의 부모가 0인 경우는 빈 게이트가 없다는 뜻으로 해석할 수 있다.
- 위 과정에서
- 공항
-
0-1 BFS
-
Suffix Array
- Suffix Array (아직 못풀음)
- 이 자료구조가 무엇인지 이해하는 것은 쉽지만, 이 구조를 활용하고, 빠른 시간내에 구축하는게 핵심인 자료구조.
- SA(Suffix Array)의 구축을 위한 naive approach는
O(n^2*log(n))이고, 좀 더 빠른 접근은O(nlog(n))에 가능함
- Suffix Array (아직 못풀음)
-
lazy propagation
-
위상 정렬 (Topology Sort)
- Cycle이 없는 directed graph가 주어질 때, 모든 노드들을 DFS를 통해 방문한 순서로 나열한 정렬 방법
a -> b -> c라면,a b c가 나와야 한다.- 즉, DFS를 통해 방문한 마지막 노드부터, 모든 노드 값을 stack에 넣고 꺼내면 된다.
stack: [c, b, a] -> a b c - 시간 복잡도는
O(V + E)(V는 노드(vertex) 개수,E는 edge 개수)
- priority queue와 노드의 indegree 값을 이용해도 위상 정렬을 수행할 수 있다.
- 어떤 노드의 indegree란, directed graph에서 그 노드로 향하는 화살표의 총 개수를 의미한다.
- 관련 문제
- 줄 세우기: 그냥 위상 정렬 알고리즘을 적용하면 됨
- Cycle이 없는 directed graph가 주어질 때, 모든 노드들을 DFS를 통해 방문한 순서로 나열한 정렬 방법
-
Floyd-Warshall algorithm
- 다익스트라 알고리즘의 단점을 보완한 알고리즘
- 다익스트라는 single source shortest path 였지만, 플로이드-워셜은 all pairs shortest path이다.
- 다익스트라는 음의 가중치를 가진 간선은 사용이 불가능하지만, 플로이드-워셜에서는 사용이 가능하다.
- 플로이드-워셜 알고리즘의 단점은 시간 복잡도가 매우 높다는 것이다 (
V^3,V는 vertex 개수) - 핵심: 플로이드-워셜은 다음과 같은 재귀식을 반복한다.
dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])- 위 식은 정점
i와j사이에k라는 정점을 통한 경로를 추가하였을 때,i와j사이의 최단 경로를 의미함
- 관련 문제
- 플로이드 : 만약 동일한 정점 간 사이의 거리가 여러개라면, 그 중 최소만 설정한다.
- 맥주 마시면서 걸어가기
- DFS, BFS로 풀어도 되지만, 플로이드-워셜 알고리즘 개념을 이용해도 풀기가 가능한 문제
- A->C 로 가는 것은 불가능(False)해도, A->B 이 가능(True)하고, B->C가 가능하다면, A->C도 가능하다.
- 다익스트라 알고리즘의 단점을 보완한 알고리즘
-
Minimum-Spanning Tree (MST) : 최소 비용 신장 트리
- 가장 적은 비용으로 그래프의 모든 노드를 연결한 트리
- 크루스칼 알고리즘: MST를 만드는 알고리즘
- 간선 간 가중치를 min-heap에 넣고, 하나씩 꺼내어 union-find를 활용해 이으면서 트리를 구성해 나간다. 트리이므로 cycle은 만들지 않도록 주의한다.
- cycle 확인 방법: union-find를 이용해서 서로 부모가 같다면 이을 필요가 없음 (이으면 cycle 발생)
- 간선 간 가중치를 min-heap에 넣고, 하나씩 꺼내어 union-find를 활용해 이으면서 트리를 구성해 나간다. 트리이므로 cycle은 만들지 않도록 주의한다.
- 관련 문제
-
재귀 함수 최대 깊이 늘리기
sys.setrecursionlimit(10**7)(메모리 초과 가능성 농후) -
ord는 character를 ascii 값으로,chr는 ascii 값을 character로 바꾸는 built-in function -
JAVA 와 같은
comparator를 이용하고 싶으면,from functools import cmp_to_key를 가져온 뒤에,
sorted(nums, key=cmp_to_key(lambda x, y: x - y)))와 같은 방법으로 정렬을 하자. (물론 따로comparator함수를 정의해도 됨) -
문제풀이 할때, 입력은
sys.readline().strip()으로 받는다.sys.readline()은 line을 전부 입력 받는 것 -
loop돌면서 특정 item 찾을 때, 못 찾을 경우 (False/True같은) temporary variable을 사용하지 않고 예외 처리 방법haystack = dict(); needle = 'a' for letter in haystack: if needle == letter: print('Found !') break else: # If no break occurred (indentation을 for loop와 같이 맞춘다.) print('Not found!')
-
sample = defaultdict(dict)은sample["a"]["b"] = 2와 같은 형태로dict내dict을 정의하게 해준다.- 또한,
defaultdict(dict)은 key가 존재하지 않을 경우, default 값을dict으로 한다.- 즉,
if "c" not in sample then sample["c"] is dict()라는 의미다. (defaultdict(list)이렇게도 가능)
- 즉,
- 또한,
-
2진수 (binary number)의 모든 1 계산하기 (
bin(i).count("1")) -
어떤 값
a에서 특정 값b를a가 0이 될 때까지 빼내기a = 5; b = 3 while a > 0: subtracted = min(a, b) # b = 3 값을 빼냄 a = max(0, a - b) # 빼낸 값 a를 조정
-
집합
a와b의 차집합은a-b로 구한다. -
입력된 값을 자동으로 정렬해주는 pure python list:
sortedcontainers.SortedList()(근데 속도가 꽤 느림, 비추천)heapq도 마찬가지로 입력된 값을 정렬해주기는 하지만,heapq로 사용되는list는 index별로 정렬되있지는 않다.add()로 데이터 입력, 다루는 건list와 똑같음,bisect사용 가능
-
리스트 정렬 시, 첫번째 원소는 오름차순, 두번재 원소는 내림차순 정렬:
array.sort(key=lambda x: (x[0], -x[1])) -
어떤 문자열이 특정 문자열로 시작하는 것을 확인하고 싶다면:
'this is test!'.startswith('this') -> True -
소수점 5 번째 자리까지 출력하는 str type 변수 만들기:
floating_num = '{:.5f}'.format(3.141592687) -
print로 출력 시,,간 간격을 수정하고 싶다면:print('<','>', sep='')-><>출력 (< >아님) -
시간에 관련된 문자열을
timeformat으로 변환k = time.strptime('2016-09-14 01:00:06', '%Y-%m-%d %H:%M:%S')- 초 단위로 변환:
time.mktime(k) # 1473782406.0
LIMIT: 테이블 가장 상위의 행 하나만 출력하기SELECT * FROM sample LIMIT 1SUM,MAX,MIN의 aggregation 을 이용해서 하나만 출력할 수 있다.
- 중복 제거
- tuple 중복에는
DISTINCT사용:SELECT DISTINCT * FROM sampleCOUNT와 중복해서 사용하는 법SELECT COUNT(DISTINCT name) FROM sample
- 특정 column 중복에는
GROUP BY사용:SELECT * FROM sample GROUP BY name
- tuple 중복에는
NULL처리NULL제거:SELECT * FROM sample WHERE name is not NULLCOUNT사용 시,NULL은 알아서 제외하고 count 함IFNULL(NULL값이면 다른 값으로 처리) :SELECT IFNULL(name, 'No name') FROM sample
- 날짜 데이터 추출
- YEAR, MONTH, DAY, HOUR, MINUTE, SECOND
- 날짜 출력 포맷 변경:
SELECT DATE_FORMAT(datetime, '%Y-%m-%d) from sample- 시/분/초 :
%h-%i-%s(%H는 24시간,%h는 12시간 단위)
- 시/분/초 :
- column 포맷 변환(
CAST):SELECT CAST(datetime AS DATE) from sample - 날짜 차이:
DATEDIFF(d1, d2)또는d1 - d2(d1가 이후 그리고 d2가 이전이여야 양수값)
- JOIN
- OUTER JOIN :
SELECT * FROM sample AS a LEFT OUTER JOIN sample_2 AS b ON a.name=b.name - INNER JOIN :
SELECT * FROM sample AS a INNER JOIN sample_2 AS b ON a.name=b.name- 다른 방법 :
SELECT * FROM sample a, sample_2 b WHERE a.name=b.name- 응용 가능 (이름이 같거나 성적이 같거나) :
SELECT * FROM sample a, sample_2 b WHERE a.name=b.name OR a.grade=b.grade
- 응용 가능 (이름이 같거나 성적이 같거나) :
- 다른 방법 :
- OUTER JOIN :
- CASE 또는 IF
- 이름에 'woo'가 들어가 있으면 'O'로 표시:
SELECT CASE WHEN name LIKE '%woo%' THEN 'O' FROM sample- IF 를 사용한 버전 (안들어가 있으면 'X' 표시도 추가):
SELECT IF(name LIKE '%woo%', 'O', 'X') FROM sample
- IF 를 사용한 버전 (안들어가 있으면 'X' 표시도 추가):
- 이름에 'woo'가 들어가 있으면 'O'로 표시:
- HAVING
- Aggregation(GROUP BY, SUM, COUNT etc.)에 조건문 처럼 쓰임
SELECT COUNT(CustomerID) FROM Customers GROUP BY Country HAVING COUNT(CustomerID) > 5
- Aggregation(GROUP BY, SUM, COUNT etc.)에 조건문 처럼 쓰임
- IN
- 특정 value에 포함된 record만 추려냄
SELECT * FROM Customers WHERE Country IN ('Germany', 'France', 'UK')SELECT * FROM Customers WHERE Country IN (SELECT Country FROM Suppliers)
- 특정 value에 포함된 record만 추려냄
- With Recursive
- 1 부터 10 까지 포함하는 테이블 만들기
with recursive f(n) as (select 1 union all select n + 1 from f where n < 10)- 사용 :
select n from f
- 1 부터 10 까지 포함하는 테이블 만들기