-
Notifications
You must be signed in to change notification settings - Fork 24
4. Using the paleopiezometry module
Warning
🚨🚨🚨 The paleopiezometry module has undergone a major change which has been incorporated in version 3.2.0. The documentation on this wiki page is intended only for version 3.2.0 and above, although it is currently incomplete. If you are using earlier versions, you can still access the old documentation using the following link: https://github.com/marcoalopez/GrainSizeTools/blob/master/DOCS/_Paleopizometry.md
The palaeopiezometry module's goals are to
- provide a comprehensive database of existing paleopiezometers (based on the average recrystallised grain size)
- automate calculations, taking into account the specifics of each piezometer (e.g. different averages used, correction factors, etc.) to avoid systematic errors
- promote reproducibility through Jupyter notebooks.
To interact with the piezometer database and perform piezometric calculations, you need to run the Python file piezometers.py, for example:
%run piezometers.pyOnce this is done, you will see a message similar to the one shown below, indicating that the piezometric database has been loaded, the version of the database, and a list of the available piezometric relationships.
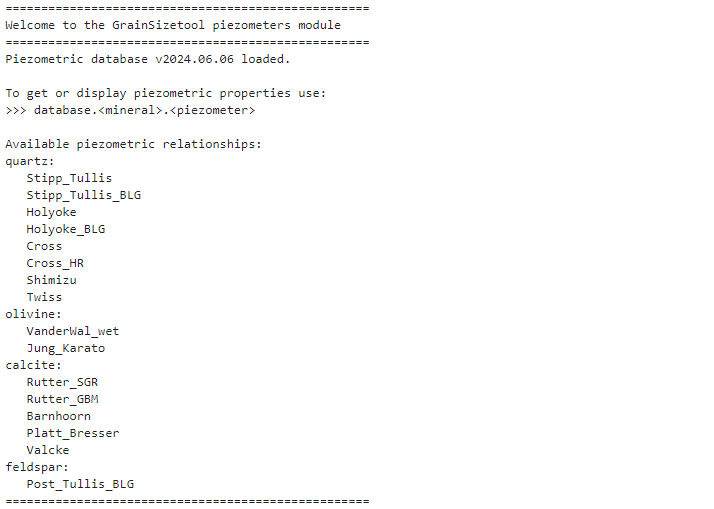
The database includes a large list of piezometric relationships of common rock-forming mineral phases such as quartz, calcite, olivine and albite. The procedure to access the properties of the different piezometric relationships is always the same:
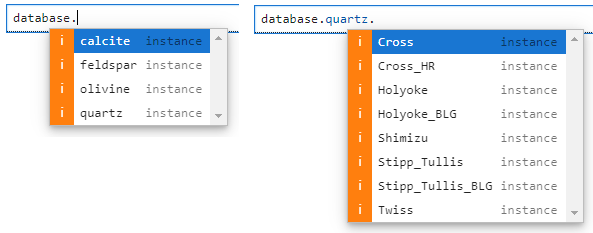
database.<mineral>.<piezometer>A handy way to quickly access the piezometers is to type database. and press the TAB key, this will open a drop down menu to select the available mineral phases. Once you set the mineral phase, add a period, e.g. database.quartz.., and press the TAB key again, this will bring up another drop down menu with all the piezometric relationships defined for that mineral phase.
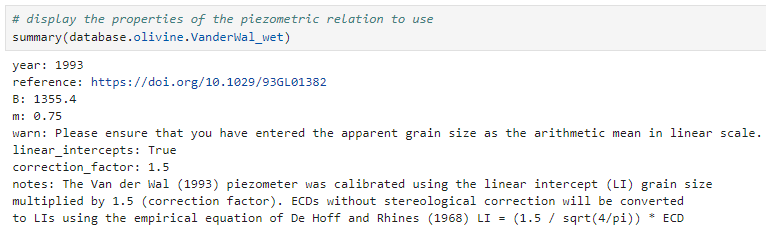
Once you press Shift + Enter and it will return all the relevant information for that piezometric relationship. If you want to present it in a better format, use the summary() function as in the following example:
There are several options for defining your own piezometric relationships. The first option is to define it in the notebook (or script) using a Python dictionary, for example:
new_olivine = {
"year": 2024,
"reference": "Unpublished",
"B": 719.7,
"m": 0.75,
"warn": "Ensure that you entered the grain size as the arithmetic mean in linear scale",
"linear_intercepts": False,
"correction_factor": False,
"notes": "Only applies to SGR recrystallization regime",
}once defined you can use it directly by calling the created object, in the example new_olivine, or even incorporate it into the general database as follows
database.olivine.my_piezometer = new_olivineIf you now type database.olivine and press "Shift + Enter" you will see that your new piezometric relationship, defined as my_piezometer in the example above, has been added to the database.
This strategy is useful for quickly testing new piezometric relationships. However, it has the disadvantage that it does not add the relationship permanently to the database, but only to the current session. If you wish to use a new piezometric relationship on a regular basis, the recommended approach is to add the relationship to the database itself. The database is located in a YALM file in the GrainSizeTools folder named piezometric_database.yalm and can be modified with any plain text editor. The structure of the YALM file looks like this:
---
database_version: 2024.06.06
metadata:
author: Marco A. Lopez-Sanchez
contact_email: marcoalopez [to be found at] outlook [dot] com
description: Piezometric database from GrainSizeTools script
created_at: 2024-06-06
license: Open Database License (ODbL) - version 1.0
usage_terms: https://opendatacommons.org/licenses/odbl/summary/
contributors:
data:
## quartz piezometers ######################################################################
quartz:
Stipp_Tullis:
year: 2003
reference: https://doi.org/10.1029/2003GL018444
B: 669.0
m: 0.79
warn: Please ensure that you have entered the apparent grain size as the root mean square (RMS).
linear_intercepts: false
correction_factor: false
notes: Only applies to recrystallization regimes 2 and 3 (SGR, GBM)
Stipp_Tullis_BLG:
year: 2003
reference: https://doi.org/10.1029/2003GL018444
B: 1264.1
m: 1.64
warn: Please ensure that you have entered the apparent grain size as the root mean square (RMS).
linear_intercepts: false
correction_factor: false
notes: Only applies to recrystallization regime 1 (BLG)
continues with more relationships...Add the desired piezometer relationship to this file, keeping the YALM format, and save the modification. The next time you run the piezometers.py file, the new ratio will already be in the database.
Important
If you want to propose the addition of a new piezometric relation to the database, I would be very happy to hear from you and expand the list of contributors and references. You are welcome to open a discussion with your suggestion(s) or to directly modify the database and make a pull request.
The GrainSizeTools script includes a method to estimate the differential stress based on the average recrystallised grain size called calc_diffstress(). This function requires
-
Define the piezometric relation to be used.
-
Enter the average (apparent) grain size calculated from equivalent circle diameters in microns. It is crucial to use a proper average without any stereological correction.
-
Specify the type of stress, either uniaxial compression/strain or plane strain, for correct stress correction.
Regarding the average grain size, the method automatically converts equivalent circular diameters to linear intercepts if applicable using the de Hoff and Rhines (1968) correction. This eliminates the need for users to worry about whether the piezometer was originally calibrated using linear intercepts. Regarding the average type, it is necessary to provide a proper grain size average to obtain a correct estimation of the differential stress. This is because each grain size-based paleopiezometer was calibrated using specific averages (e.g. the arithmetic mean, median or RMS mean to name some examples). Additionally, please do not not apply any form of stereological correction to the estimation of the average grain size. In the event that the author(s) of the piezometer used any form of stereological correction, the average grain size will be automatically corrected by the method, which will issue a warning when the correction has been done.
The third requirement is for the user to decide whether to apply the Paterson and Olgaard (2000) correction factor to the estimate of the differential stress for plane stress. This is because the experiments used to calibrate piezometers were performed under uniaxial compression, while natural shear zones behave as plane stress volumes.
Note
Historically, researchers have used various techniques to measure apparent grain size, such as line intercept or equivalent diameter measurements, and different types of averages (e.g. arithmetic mean, median, root mean square, etc.), which are not directly comparable. In addition to this, different types of correction factors have been used and, to complicate matters further, there are several methods of calculating line intercepts and equivalent diameter measurements which also do not give equivalent results and are often not explicitly stated in the original articles. This has made the correct use of a paleopiezometer and especially the comparison of results between different paleopiezometers a nightmare. GrainSizeTools tries to correct this by making the input the same for all piezometric relationships and warning you of the corrections made.
An example of using a piezometric relationship to estimate the paleostress would be as follows:
calc_diffstress(
piezometer=database.olivine.VanderWal_wet,
grain_size=140,
correction=True
)In this example, the Van der Wal olivine piezometer was used, an average grain size of 140 microns was set and the correction factor of Paterson and Olgaard (2000) was activated. Once the cell has been run, we will see a result like the following:
Calculated differential stress = 31.06 MPa
INFO:
Please ensure that you have entered the apparent grain size as the arithmetic mean in linear scale.
The diameters have been converted to linear intercepts using the de Hoff and Rhines (1968) correction.
The differential stress was corrected for plane stress using the methodology outlined in Paterson and Olgaard (2000).👉 TODO...
👉 TODO...
Caution
Never combine averages -or any other statistic- as if they were data points. In the context of meta-analysis, which is a statistical procedure for combining data from multiple studies or experiments, a common mistake is to take different estimates and averaged them. However, the stress estimates are already an average and calculating a mean of the averages is mathematically incorrect because this approach ignores the uncertainty of the average. Similarly, to look at the raw grain size data from all the grain maps and make the estimate from there is also incorrect because this ignores the uncertainty within and between experimental conditions. The correct procedure here is to take the weighted mean of the averages, where each mean is weighted by its variance or the squared standard error of the mean (SEM). The averages module of the GrainSizeTools script has a function to do this named weighted_mean_and_se()