-
Notifications
You must be signed in to change notification settings - Fork 5
Theoretical aspects ptp
Given a rooted binary tree T=(V,E), we want to partition its tips into disjoint sets (putative species). We denote the set of branches in the tree belonging to the subtree of species i by Ei. We assume that the branch lengths of each species follow an exponential distribution. We fit the between species edges, denoted by Es, to an exponential process as well. In both PTP and mPTP, we then want to find a delimitation that maximizes the likelihood of the partition of branch lengths.
In the single-rate PTP model, all species share the same lambda. This means that every species evolved with the same rate. More formally, we want to maximize the likelihood
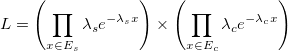
In single-rate PTP, we compare the maximum likelihood delimitation obtaining by the heuristic to the null model. The null model is a delimitation that groups all tips of the tree into one single species. We perform a p-value test in order to decide whether to keep the null model or reject the null model and use the maximum likelihood delimitation instead.
In the mPTP model, each species has its own lambda. This means that we assume for each species a different rate. In this case, we want to maximize the likelihood
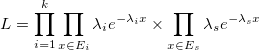
Since multi-rate mPTP compares models with a different number of parameters (as there is a separate lambda for each species), we cannot use the p-value test in mPTP. Instead, we use the Akaike Information Criterion to decide which number of species fits best to the given data (the tree). This approach avoids oversplitting the taxa into too many species.