This repository contains fast cubic spline interpolation written in Java and Matlab, implementing code from the paper of Haysn Hornbeck "Fast Cubic Spline Interpolation".
The original python code is available here.
The motivation for this code is described in the paper, but basically it is Creative Commons Zero license analogue of Numerical Recipes procedure.
The general idea behind is that given N tabulated knots xi (x0,x1,...,xN-1 so that x0<x1<...<xN-1)
and function values yi at those points, code builds interpolating piece-wise cubic spline passing through those points.
This interpolation is smooth in first derivative and continuous in the second derivative.
(BTW, for a general spline "getting started" I highly recommend this great video).
To build this interpolation, one of the two extra assumptions at boundaries are needed:
- The second derivatives at the end points are equal to zero (functions CubicSpline(x,y) in java and cubicspline(x,y,xs) in matlab). In this case it is so called natural cubic spline. Or
- The first derivatives at the end points are provided by user (functions CubicSpline(x,y,start_deriv,end_deriv) in java and cubicspline(x,y,start_deriv,end_deriv,xs) in matlab).
Well, in practice, it is possilbe to mix them: for one end second derivative is zero and specify derivative for the second end. Then for the first end just supply a large (Double.MAX or Inf) value of the first derivative.
This code is actually a bit extended version. There are two additions:
- There is a possibility to estimate first derivatives from the provided data at end points. Calling functions CubicSpline(x,y,n_est) in java and cubicspline(x,y,n_est,xs) in matlab estimates derivatives values using n_est boundary points for each end. It is done by finite difference method, where coefficients are calculated from this paper. The xi values does not have to be equidistant.
- Apart from evaluation of spline itself at interpolation points, there is a new routine to calculate spline's derivative (slope) at those points (evalSlope functions).
Some extra notes:
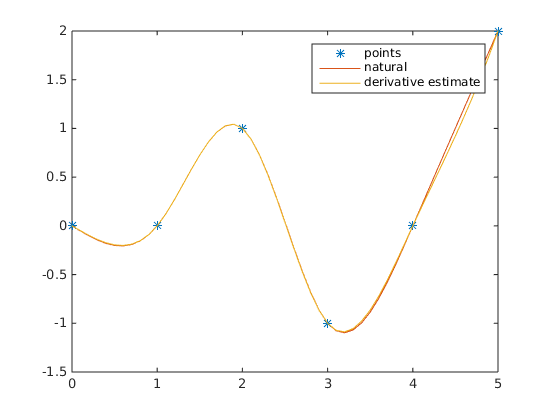
The usage of code is illustrated in "example.m" file. Here is interpolation with natural vs estimated first derivatives:
And calculated slopes (derivatives, tangents) shown as arrows on top of the second spline:
The main package/class is cubicspline/CubicSpline. This repo also contains comparison of this implementation with the one used in ImageJ (cubicsplineIJ/CubicSplineImageJ). And test package to validate main class against Matlab/ImageJ routines.
Email katpyxa @ gmail.com for any questions/comments/suggestions.