19

Дана переменная-отношение R(A, B, C, D) с функциональными зависимостями S={A–>BC, B–>C, A–>B, AB–>C, AC–>D}. Найти неприводимое множество функциональных зависимостей, эквивалентное данному множеству.

(min покрытие == ФЗ (функциональные зависимости) явл. неприводимым)

Множество ФЗ явл. неприводимым (min покрытие) тогда и только тогда, когда обладает след. свойствами:

Детерминант - левая часть. Зависимая часть - правая.

1. Для любой ФЗ X->Y, Y - один элемент.
2. Ни одну ФЗ нельзя удалить без изменения замыкания. (Пробуем удалить и смотрим на замыкание, поменялось?)
3. Ни один атрибут не может быть удален из детирминанта без изменения замыкания

1.
S =
{
A --> B,
A --> C,
B --> C,
A --> B, (Выше уже есть, удаляем)
AB --> C,
AC --> D
}

2.1 Удаляем зависимость A --> C потому что выводима:

A --> B, B --> C => A --> C

S = {A --> B,B --> C,AB --> C, AC --> D}

2.2 Удаляем AB --> C Потому что выводима:

A --> B, B --> C => AB --> BC

AB --> BC => AB --> C, AB --> B (Вывели)

S = {A --> B,B --> C, AC --> D}

3. Удаляем атрибут из AC --> D и пытаемся вывести AC --> D.

(Удалили C):

A --> D, A --> C (Это у нас есть(можно вывести)) => A --> DC
AС --> DC => AС --> D, AС --> C 

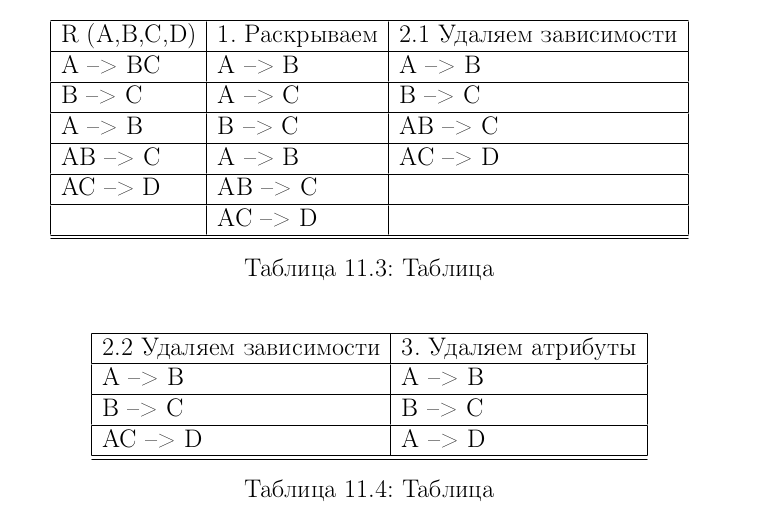
Поэтапное решение:

<- or ->