Beveling

Here we provide some additional detail about the bevel operations and their implementation in Scotty3D. Each bevel operation has two components:

1. a method that modifies the connectivity of the mesh, creating new beveled elements, and
2. a method the updates the geometry of the mesh, insetting and offseting the new vertices according to user input.

The methods that update the connectivity are HalfedgeMesh::bevelVertex, halfedgeMesh::bevelEdge, and HalfedgeMesh::bevelFace. The methods that update geometry are HalfedgeMesh::bevelVertexComputeNewPositions, HalfedgeMesh::bevelEdgeComputeNewPositions, and HalfedgeMesh::bevelFaceComputeNewPositions. The methods for updating connectivity can be implemented following the general strategy outlined in the tutorial above. Note that the methods that update geometry will be called repeatedly for the same bevel, in order to adjust positions according to user mouse input. See the gif in the User Guide.

To update the geometry of a beveled element, you are provided with the following data:

• originalVertexPosition(s) - These are the original vertex positions of the mesh element, before any insetting or offsetting is applied.
• newHalfedges - These are the halfedges "around" the element currently being beveled.
• tangentialInset - The amount by which the new face should be inset (i.e., "shrunk" or "expanded")
• normalShift (faces only) - The amount by which the new face should be offset in the normal direction.

More specifically, the array newHalfedges stores the following data:

• For a beveled vertex, newHalfedges stores the halfedges pointing from the vertices of the new polygon to the neighbors of the original vertex.
• For a beveled edge, newHalfedges stores the halfedges pointing from the vertices of the new polygon to the neighbors of the original edge endpoints.
• For a beveled face, newHalfedges stores the halfedges pointing from the vertices of the new polygon to the vertices of the original polygon.

These relationships are illustrated by the following diagram:

The basic recipe for updating the vertex positions is then:

• Iterate over the list of halfedges (newHalfedges)
• Grab the vertex coordinates that are needed to compute the new, updated vertex coordinates (this could be a mix of values from originalVertexPositions, or the members Vertex::position)
• Compute the updated vertex positions using the current values of tangentialInset (and possibly normalShift)
• Store the new vertex positions in Vertex::position for the vertices of the new, beveled polygon only (i.e., the positions of any polygon "outside" the dark blue one in the figures above should not be updated)

The reason for storing newHalfedges and originalVertexPositions in an array is that it makes it easy to access positions "to the left" and "to the right" of a given vertex. For instance, suppose we want to figure out the offset from the corner of a polygon. We might want to compute some geometric quantity involving the three vertex positions orig[i-1], orig[i], and orig[i+1] (as well as inset), then set the new vertex position hs[i]->vertex()->position to this new value:

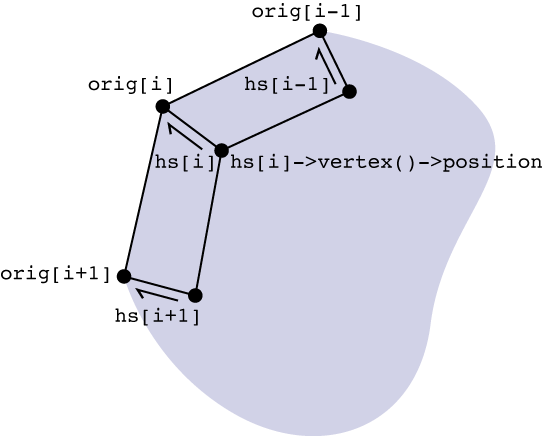
A useful trick here is modular arithmetic: since we really have a "loop" of vertices, we want to make sure that indexing the next element (+1) and the previous element (-1) properly "wraps around." This can be achieved via code like

// Get the number of vertices in the new polygon
int N = hs.size();

// Assuming we're looking at vertex i, compute the indices
// of the next and previous elements in the list using
// modular arithmetic---note that to get the previous index,
// we can't just subtract 1 because the mod operation in C++
// doesn't behave quite how you might expect for negative
// values!
int a = (i+N-1) % N;
int b = i;
int c = (i+1) % N;

// Get the actual 3D vertex coordinates at these vertices
Vector3D pa = orig[a];
Vector3D pb = orig[b];
Vector3D pc = orig[c];

From here, you will need to compute new coordinates for vertex i, which can be accessed from hes[i]->vertex()->position. As a "dummy" example (i.e., this is NOT what you should actually do!!) this code will set the position of the new vertex to the average of the vertices above:

hes[i].vertex()->position = ( pa + pb + pc ) / 3.; // replace with something that actually makes sense!

The only question remaining is: where should you put the beveled vertex? We will leave this decision up to you. This question is one where you will have to think a little bit about what a good design would be. Questions to ask yourself:

• How do I compute a point that is inset from the original geometry?
• For faces, how do I shift the geometry in the normal direction? (You may wish to use the method Face::normal() here.)
• What should I do as the offset geometry starts to look degenerate, e.g., shrinks to a point, or goes outside some reasonable bounds?
• What should I do when the geometry is nonplanar?
• Etc.

The best way to get a feel for whether you have a good design is to try it out! Can you successfully and easily use this tool to edit your mesh? Or is it a total pain, producing bizarre results? You be the judge!