Triangulation

A variety of geometry processing algorithms become easier to implement (or are only well defined) when the input consists purely of triangles. The method HalfedgeMesh::triangulate converts any polygon mesh into a triangle mesh by splitting each polygon into triangles. This transformation is performed in-place, i.e., the original mesh data is replaced with the new, triangulated data (rather than making a copy). The triangulate method is basically just a wrapper around HalfedgeMesh::splitPolygon, which splits a single face f into triangles. The implementation of this method will look much like the implementation of the local mesh operations (see the tutorial above).

There is more than one way to split a polygon into triangles. Two common patterns are to connect every vertex to a single vertex, or to "zig-zag" the triangulation across the polygon:

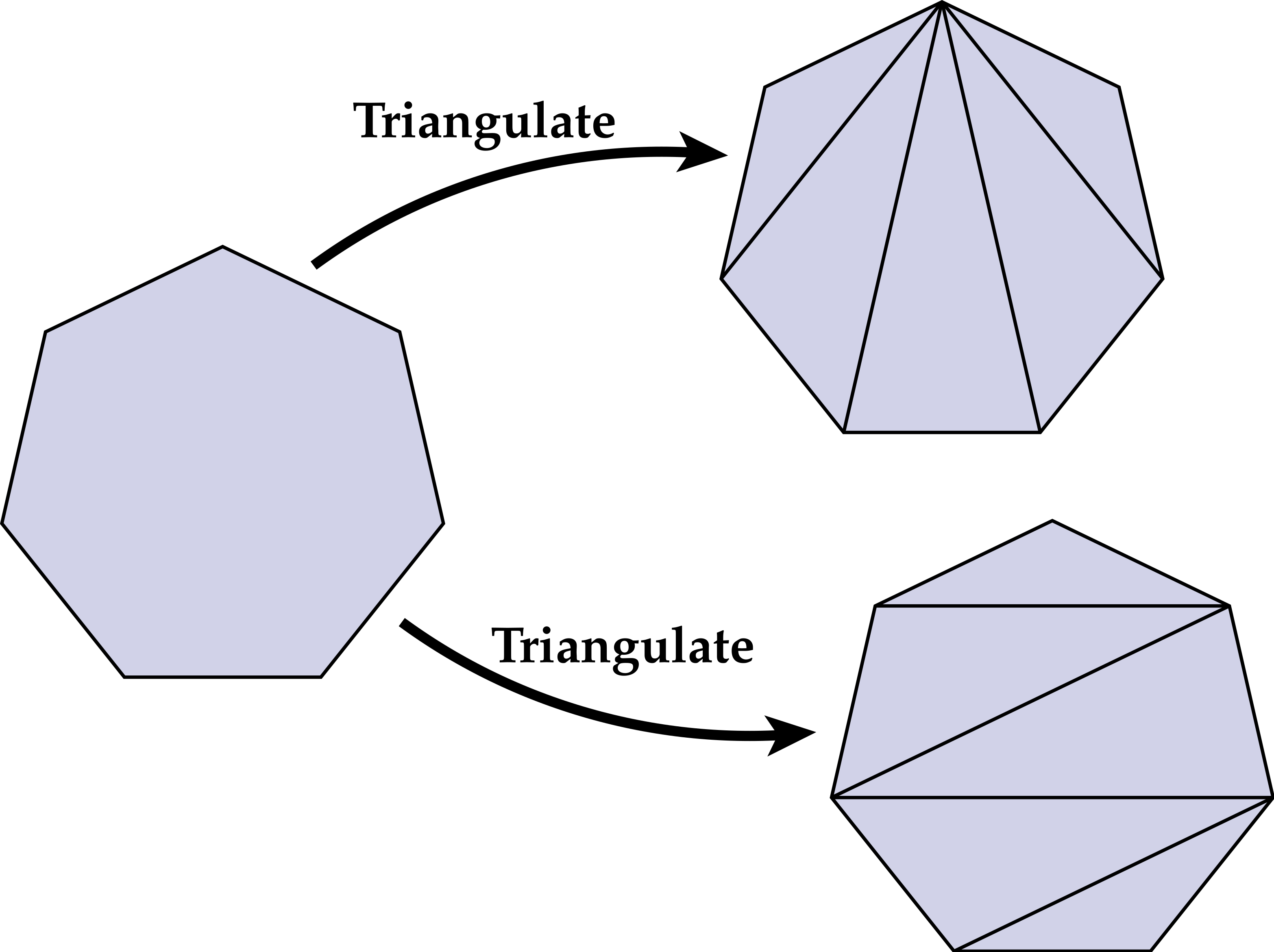
The splitPolygon routine is not required to produce any particular triangulation so long as:

• all polygons in the output are triangles,
• the vertex positions remain unchanged, and
• the output is a valid, manifold halfedge mesh.

Note that triangulation of nonconvex or nonplanar polygons may lead to geometry that is unattractive or difficult to interpret. However, the purpose of this method is simply to produce triangular connectivity for a given polygon mesh, and correct halfedge connectivity is the only invariant that must be preserved by the implementation. The geometric quality of the triangulation can later be improved by running other global algorithms (e.g., isotropic remeshing); ambitious developers may also wish to consult the following reference:

• Zou et al, "An Algorithm for Triangulating Multiple 3D Polygons"